题目内容
如图1,边长为5的正方形ABCD是20×20等距网格图,E是AB的中点,DE将正方形ABCD分成明暗两部分.线段MN的长度为5,MN的初始位置与AB重合.点M在AB上滑动,点N在BC上滑动,且MN的长度保持不变.
(1)如图2,当AM等于1时,MN与DE相交于点O,求ON的长;
(2)如图3,设AM=x,BN=t,MN落在明区部分的长度为y,试用x,t表示y;
(3)观察图1、2、3、4,说明y随x的变化情况.
【答案】分析:(1)过点O作OF∥AD交AB于F,根据△EOF和△EDA相似求出OF=2EF,设EF=a,表示出MF、OF,再根据AM=1,求出BM,然后利用勾股定理列式求出BN,然后根据△MFO和△MBN相似,利用相似三角形对应边成比例列式求出a的值,再求出MO:ON,利用勾股定理列式求出MN=5,然后求解即可;
(2)过点O作OF∥AD交AB于F,然后与(1)的思路相同求解即可;
(3)观察图形,分点M在点E上方与下方两种情况解答.
解答:解:(1)如图2,过点O作OF∥AD交AB于F,
则△EOF∽△EDA,
∴ =
= ,
,
∵E是AB的中点,
∴AE=BE= AB=
AB= ×5=2.5,
×5=2.5,
∴ =
= ,
,
∴OF=2EF,
设EF=a,则MF=AE-AM-EF=2.5-1-a=1.5-a,
OF=2a,
∵AM=1,
∴BM=5-1=4,
根据勾股定理,BN= =
= =3,
=3,
∵OF∥AD∥BC,
∴△MFO∽△MBN,
∴ =
= ,
,
即 =
= ,
,
解得a= ,
,
∴MF=1.5- =
= ,
,
BF=a+2.5= +2.5=
+2.5= ,
,
∴ =
= =
= =
= ,
,
∴ON=5× =
= ;
;

(2)如图3,过点O作OF∥AD交AB于F,
与(1)的解法相同,设EF=a,则MF=2.5-a-x,
OF=2a,
∵OF∥AD∥BC,
∴△MFO∽△MBN,
∴ =
= ,
,
即 =
= ,
,
解得a= ,
,
∴ =
= ,
,
即 =
= ,
,
解得y= ;
;
(3)由图可知,当0<x≤2.5时,y随x增大而增大,
当2.5<x<5时,y不再变化,为MN的长,是5.
(说明:在(3)中,不论学生用“<”,还是“≤”,只要分段正确,均不扣分;若注意区分“<”和“≤”的用法,则酌情加1~4分)
点评:本题考查了相似三角形的判定与性质,作辅助线构造出相似三角形是解题的关键,难点在于利用好中间量OF,运算量较大,计算时要认真仔细.
(2)过点O作OF∥AD交AB于F,然后与(1)的思路相同求解即可;
(3)观察图形,分点M在点E上方与下方两种情况解答.
解答:解:(1)如图2,过点O作OF∥AD交AB于F,
则△EOF∽△EDA,
∴
 =
= ,
,∵E是AB的中点,
∴AE=BE=
 AB=
AB= ×5=2.5,
×5=2.5,∴
 =
= ,
,∴OF=2EF,
设EF=a,则MF=AE-AM-EF=2.5-1-a=1.5-a,
OF=2a,
∵AM=1,
∴BM=5-1=4,
根据勾股定理,BN=
 =
= =3,
=3,∵OF∥AD∥BC,
∴△MFO∽△MBN,
∴
 =
= ,
,即
 =
= ,
,解得a=
 ,
,∴MF=1.5-
 =
= ,
,BF=a+2.5=
 +2.5=
+2.5= ,
,∴
 =
= =
= =
= ,
,∴ON=5×
 =
= ;
;
(2)如图3,过点O作OF∥AD交AB于F,
与(1)的解法相同,设EF=a,则MF=2.5-a-x,
OF=2a,
∵OF∥AD∥BC,
∴△MFO∽△MBN,
∴
 =
= ,
,即
 =
= ,
,解得a=
 ,
,∴
 =
= ,
,即
 =
= ,
,解得y=
 ;
;(3)由图可知,当0<x≤2.5时,y随x增大而增大,
当2.5<x<5时,y不再变化,为MN的长,是5.
(说明:在(3)中,不论学生用“<”,还是“≤”,只要分段正确,均不扣分;若注意区分“<”和“≤”的用法,则酌情加1~4分)
点评:本题考查了相似三角形的判定与性质,作辅助线构造出相似三角形是解题的关键,难点在于利用好中间量OF,运算量较大,计算时要认真仔细.

练习册系列答案
相关题目
如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
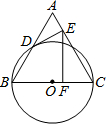 如图,以边长为4的正△ABC的BC边为直径作⊙O与AB相交于点D,⊙O的切线DE交AC于E,EF⊥BC,点F是垂足,则EF=
如图,以边长为4的正△ABC的BC边为直径作⊙O与AB相交于点D,⊙O的切线DE交AC于E,EF⊥BC,点F是垂足,则EF=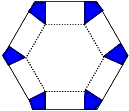 如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为
如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
 如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )
如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )