题目内容
如图,AB是⊙O的直径,C是AB延长线上一点,且BC=OB,CE与⊙O交于点D,过点A作AE⊥CE,垂足为E,连接AD,∠DAC=∠C.
(Ⅰ)求证:直线CE是⊙O的切线.
(Ⅱ)求
的值.
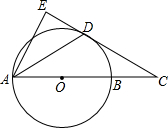
(Ⅰ)求证:直线CE是⊙O的切线.
(Ⅱ)求
| CD |
| DE |

(Ⅰ)∵AB为圆O的直径,
∴∠ADB=90°,
∵∠DAC=∠C,
∴AD=CD,
∵BC=OB,
∴AB=OC,
在△ADB和△COD中,
,
∴△ADB≌△COD(SAS),
∴∠ADB=∠ODC=90°,
则直线CE是圆O的切线;
(Ⅱ)由第一问得到OD⊥CE,
又∵AE⊥CE,
∴OD∥AE,
∴
=
,
∵BC=OB=
OC,OA=OB,
∴
=
=
=
=2.

∴∠ADB=90°,
∵∠DAC=∠C,
∴AD=CD,
∵BC=OB,
∴AB=OC,
在△ADB和△COD中,
|
∴△ADB≌△COD(SAS),
∴∠ADB=∠ODC=90°,
则直线CE是圆O的切线;
(Ⅱ)由第一问得到OD⊥CE,
又∵AE⊥CE,
∴OD∥AE,
∴
| CD |
| DE |
| OC |
| OA |
∵BC=OB=
| 1 |
| 2 |
∴
| CD |
| DE |
| OC |
| OA |
| OC |
| OB |
| 2 |
| 1 |


练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目