题目内容
【题目】已知过点A(0,1)的椭圆C: ![]() +
+ ![]() =1(a>b>0)的左右焦点分别为F1、F2 , B为椭圆上的任意一点,且
=1(a>b>0)的左右焦点分别为F1、F2 , B为椭圆上的任意一点,且 ![]() |BF1|,|F1F2|,
|BF1|,|F1F2|, ![]() |BF2|成等差数列.
|BF2|成等差数列.
(1)求椭圆C的标准方程;
(2)直线l:y=k(x+2)交椭圆于P,Q两点,若点A始终在以PQ为直径的圆外,求实数k的取值范围.
【答案】
(1)
解:∵ ![]() |BF1|,|F1F2|,
|BF1|,|F1F2|, ![]() |BF2|成等差数列,
|BF2|成等差数列,
∴2|F1F2|= ![]() |BF1|+
|BF1|+ ![]() |BF2|=
|BF2|= ![]() (|BF1|+|BF2|),
(|BF1|+|BF2|),
由椭圆定义得22c= ![]() 2a,
2a,
∴c= ![]() a;
a;
又椭圆C: ![]() +
+ ![]() =1(a>b>0)过点A(0,1),
=1(a>b>0)过点A(0,1),
∴b=1;
∴c2=a2﹣b2=a2﹣1= ![]() a2,
a2,
解得a=2,c= ![]() ;
;
∴椭圆C的标准方程为 ![]() +y2=1;
+y2=1;
(2)
解:设P(x1,y1),Q(x2,y2)
联立方程 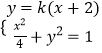 ,消去y得:
,消去y得:
(1+4k2)x2+16k2x+(16k2﹣4)=0;
依题意直线l:y=k(x+2)恒过点(﹣2,0),此点为椭圆的左顶点,
∴x1=﹣2,y1=0,﹣﹣﹣﹣①
由方程的根与系数关系可得,x1+x2= ![]() ;②
;②
可得y1+y2=k(x1+2)+k(x2+2)=k(x1+x2)+4k;③
由①②③,解得x2= ![]() ,y2=
,y2= ![]() ;
;
由点A在以PQ为直径的圆外,得∠PAQ为锐角,即 ![]()
![]() >0;
>0;
由 ![]() =(﹣2,﹣1),
=(﹣2,﹣1), ![]() =(x2,y2﹣1),
=(x2,y2﹣1),
∴ ![]()
![]() =﹣2x2﹣y2+1>0;
=﹣2x2﹣y2+1>0;
即 ![]() +
+ ![]() ﹣1<0,
﹣1<0,
整理得,20k2﹣4k﹣3>0,
解得:k<﹣ ![]() 或k>
或k> ![]() ,
,
∴实数k的取值范围是k<﹣ ![]() 或k>
或k> ![]()
【解析】(1)由题意,利用等差数列和椭圆的定义求出a、c的关系,再根据椭圆C过点A,求出a、b的值,即可写出椭圆C的标准方程;(2)设P(x1 , y1),Q(x2 , y2),根据题意知x1=﹣2,y1=0;联立方程 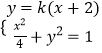 消去y,由方程的根与系数关系求得x2、y2 , 由点A在以PQ为直径的圆外,得∠PAQ为锐角,
消去y,由方程的根与系数关系求得x2、y2 , 由点A在以PQ为直径的圆外,得∠PAQ为锐角, ![]()
![]() >0;由此列不等式求出k的取值范围.
>0;由此列不等式求出k的取值范围.


