��Ŀ����
����Ŀ�������龰��һ����ѧ�κ���ʦ������һ����ϰ�⣺
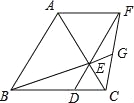
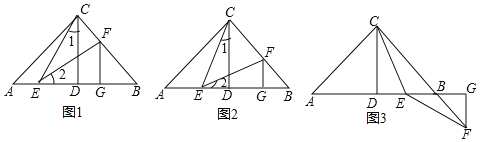
��ͼ1����֪Rt��ABC�У�AC��BC����ABC��90�㣬CD��AB�ڵ�D����E��F�ֱ���AD��BC�ϣ���1����2��FG��AB�ڵ�G����֤����CDE�ա�EGF
��1���Ķ����⣬��ɽ�𣺱���֤����˼·���������п�ͼ��ʾ��
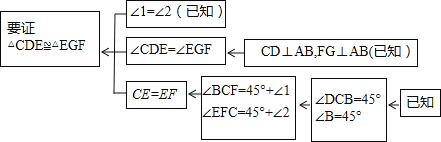
��������˼·������������д�������ϰ���֤�����̣�
��2������λ�ã�֤�����ۣ���ͼ2����CEƽ�֡�ACD�������������䣬�ж�AE��BF��������ϵ����˵�����ɣ�
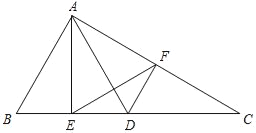
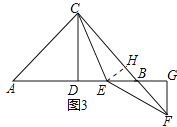
��3��֪ʶǨ�ƣ�̽�����֣���ͼ3����֪��Rt��ABC�У�AC��BC����ACB��90�㣬CD��AB�ڵ�D������E��DB���е㣬��F��ֱ��CB�ϣ���EC��EF����ֱ��д��BF��AE��������ϵ��������д�����̣�
���𰸡���1������������2��AE��BF�����ɼ���������3��AE��![]() BF��
BF��
��������
��1����֤��CE��EF������AAS����֤����CDE�ա�EGF��AAS��������
��2����֤��ACE����2����֤����ACE�ա�BEF��AAS�������ɵ�֤AE��BF��
��3����EH��BC��H����DE��x�����AE��3x����֤��BF��![]() x�����ɵó�������
x�����ɵó�������
��1��֤������AC��BC����ACB��90�㣬
���A����B��45�㣬
��CD��AB��
���CDB��90�㣬
���DCB��45�㣬
�ߡ�ECF����DCB+��1��45��+��1����EFC����B+��2��45��+��2����1����2��
���ECF����EFC��
��CE��EF��
��CD��AB��FG��AB��
���CDE����EGF��90�㣬
�ڡ�CDE�͡�EGF�У�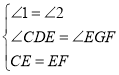 ��
��
���CDE�ա�EGF��AAS����
��2��֤�����ɣ�1���ã�CE��EF����A����B��
��CEƽ�֡�ACD��
���ACE����1��
�ߡ�1����2��
���ACE����2��
�ڡ�ACE�͡�BEF�У�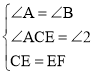 ��
��
���ACE�ա�BEF��AAS����
��AE��BF��
��3���⣺AE��![]() BF����EH��BC��H����ͼ3��ʾ��
BF����EH��BC��H����ͼ3��ʾ��
��DE��x����������ã�BE��DE��x��AD��BD��2x��CD��AD��2x��AE��3x��
���ݹ��ɶ����ã�BC��AC��2![]() x��
x��
�ߡ�ABC��45�㣬EH��BC��
��BH��![]() x��
x��
��CH��BC��BH��![]() x��
x��
��EC��EF��
��FH��CH��![]() x��
x��
��BF��![]() x��
x��![]() x��
x��![]() x��
x��
��![]() ��
��![]() ��
��![]() ��
��
��AE��![]() BF��
BF��

 Сѧ��10���ӿ������100��ϵ�д�
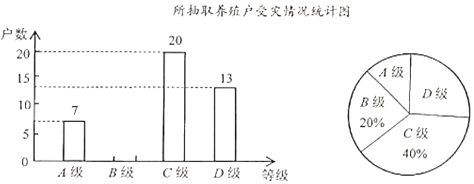
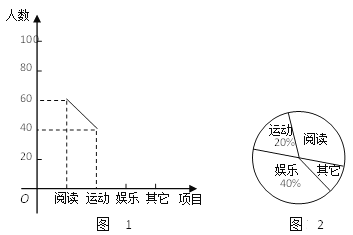
Сѧ��10���ӿ������100��ϵ�д�����Ŀ��ijѧУ�����ͳ��������꼶����600��ͬѧ��Ϊ�˿�����������֪ʶ��ѧУ��֯��һ������֪ʶ������С��ֱ�ӳ��������������꼶�����ȡ��40��ͬѧ�ijɼ����ٷ��ƣ����������ݣ��ɼ������������������ͷ�������������˲�����Ϣ��
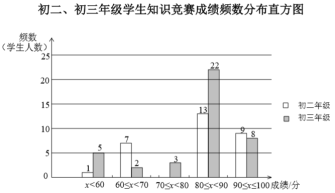
![]() �������������꼶ѧ��֪ʶ�����ɼ���������Ƶ���ֲ�ֱ��ͼ���£����ݷֳ�5�飺
�������������꼶ѧ��֪ʶ�����ɼ���������Ƶ���ֲ�ֱ��ͼ���£����ݷֳ�5�飺![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����
![]() �������꼶ѧ��֪ʶ�����ɼ���
�������꼶ѧ��֪ʶ�����ɼ���![]() ��һ����������£�
��һ����������£�
80 80 81 83 83 84 84 85 86 87 88 89 89
![]() ������������ѧ��֪ʶ�����ɼ���ƽ��������λ�����������£�
������������ѧ��֪ʶ�����ɼ���ƽ��������λ�����������£�
ƽ���� | ��λ�� | ���� | |
�����꼶 | 80.8 |
| 96.9 |
�����꼶 | 80.6 | 86 | 153.3 |
����������Ϣ���ش��������⣺
��1����ȫ�����֪ʶ�����ɼ�Ƶ���ֲ�ֱ��ͼ��
��2��д������![]() ��ֵ��
��ֵ��
��3��![]() ͬѧ������������Ϣ��˵�Լ��ijɼ����ڱ��꼶����ǰ40%��
ͬѧ������������Ϣ��˵�Լ��ijɼ����ڱ��꼶����ǰ40%��![]() ͬѧ����
ͬѧ����![]() ͬѧ�ijɼ���˵�������ź�����ijɼ��������꼶������ǰ50%�������ж�
ͬѧ�ijɼ���˵�������ź�����ijɼ��������꼶������ǰ50%�������ж�![]() ͬѧ��________������������������꼶��ѧ�����жϵ�������________��
ͬѧ��________������������������꼶��ѧ�����жϵ�������________��
��4�����ɼ���85�ּ�����Ϊ���㣬����Ƴ����꼶�����ɼ����������Ϊ____��