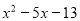题目内容
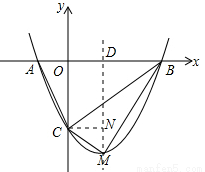
(12分)如图,抛物线y=mx2―2mx―3m(m>0)与x轴交于A、B两点, 与y轴交于C点。

(1)请求抛物线顶点M的坐标(用含m的代数式表示),A,B两点的坐标;(6分)
(2)经探究可知,△BCM与△ABC的面积比不变,试求出这个比值;(6分)
(1)M的坐标为(1, m),A,B两点的坐标为(-1,0)、(3,0) (2)1:2
m),A,B两点的坐标为(-1,0)、(3,0) (2)1:2
【解析】
试题分析:(1)将抛物线的解析式化为顶点坐标式,即可得到顶点M的坐标;抛物线的解析式中,令y=0,可求得A、B的坐标.
(2)易求得C点坐标,即可得到OC的长,以AB为底,OC为高,即可求出△ABC的面积;△BCM的面积无法直接求得,可用割补法求解,过M作MD⊥x轴于D,根据B、C、M四点坐标,可分别求出梯形OCMD、△BDM的面积,它们的面积和减去△BOC的面积即为△BCM的面积,进而可得到△ABC、△BCM的面积比
试题解析:(1)∵y=mx2―2mx―3m=m(x2―2x―3)=m(x-1)2―4m,
∴抛物线顶点M的坐标为(1,-4m),
∵抛物线y=mx2―2mx―3m(m>0)与x轴交于A、B两点,
∴当y=0时,mx2―2mx―3m=0,
∵m>0,
∴x2―2x―3=0,
解得x1=-1,x,2=3,
∴A,B两点的坐标为(-1,0)、(3,0).
(2)当x=0时,y=―3m,
∴点C的坐标为(0,-3m),
∴S△ABC=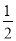 ×|3-(-1)|×|-3m|=6|m|=6m,
×|3-(-1)|×|-3m|=6|m|=6m,
过点M作MD⊥x轴于D,
则OD=1,BD=OB-OD=2,
MD=|-4m |=4m.
∴S△BCM=S△BDM+S梯形OCMD-S△OBC
=
=
=3m.
∴S△BCM:S△ABC=1:2
考点:二次函数的综合题
考点分析: 考点1:二次函数 定义:一般地,如果
 (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。 ①所谓二次函数就是说自变量最高次数是2;
②二次函数
 (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。③二次函数
 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式: (1)一般式:
 (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0); (2)顶点式:
 (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0) (3)当抛物线
 与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。 二次函数的一般形式的结构特征:
①函数的关系式是整式;
②自变量的最高次数是2;
③二次项系数不等于零。 二次函数的判定:
二次函数的一般形式中等号右边是关于自变量x的二次三项式;
当b=0,c=0时,y=ax2是特殊的二次函数;
判断一个函数是不是二次函数,在关系式是整式的前提下,如果把关系式化简整理(去括号、合并同类项)后,能写成
 (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
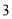 B.0 C.
B.0 C. D.2014
D.2014  = 3的相反数是 的倒数是-2
= 3的相反数是 的倒数是-2
 的和是
的和是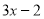 ,则这个多项式为( )
,则这个多项式为( ) (B)
(B)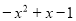
 (D)
(D)