Question

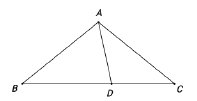
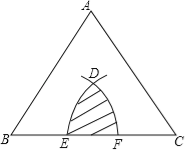
【题目】如图，正三角形ABC的边长是2，分别以点B，C为圆心，以r为半径作两条弧，设两弧与边BC围成的阴影部分面积为S，当≤r＜2时，S的取值范围是　 　．

Answer 1

【答案】≤S＜

【解析】

首先求出S关于r的函数表达式，分析其增减性；然后根据r的取值，求出S的最大值与最小值，从而得到S的取值范围．

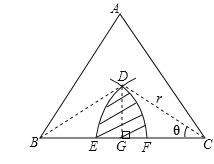
解：如右图所示，过点D作DG⊥BC于点G，易知G为BC的中点，CG=1．

在Rt△CDG中，由勾股定理得：DG==．

设∠DCG=θ，则由题意可得：

S=2（S扇形CDE﹣S△CDG）=2（﹣×1×）=﹣，

∴S=﹣．

当r增大时，∠DCG=θ随之增大，故S随r的增大而增大．

当r=时，DG==1，∵CG=1，故θ=45°，

∴S=﹣=﹣1；

若r=2，则DG==，∵CG=1，故θ=60°，

∴S=﹣=﹣．

∴S的取值范围是：﹣1≤S＜﹣．

故答案为：﹣1≤S＜﹣．