题目内容
在锐角三角形纸片ABC中,BC=4,高AD=3,直线EF∥BC,分别交线段AB,AC,AD于E,F,G,设EF=x.
(1)求线段AG的长(用含x的代数式表示);
(2)将纸片沿直线EF折叠,设点A落在平面上的点为P,△PEF与四边形BCFE重叠部分的面积为y,求y关于x的函数关系式,并写出x的取值范围.
(1)求线段AG的长(用含x的代数式表示);
(2)将纸片沿直线EF折叠,设点A落在平面上的点为P,△PEF与四边形BCFE重叠部分的面积为y,求y关于x的函数关系式,并写出x的取值范围.
分析:(1)利用EF∥BC,得出△AEF∽△ABC,进而得出
=
,求出即可;
(2)根据当0<x≤2时,当2<x<4时,分别利用三角形面积求法以及相似三角形的性质得出即可.
| AG |
| AD |
| EF |
| BC |
(2)根据当0<x≤2时,当2<x<4时,分别利用三角形面积求法以及相似三角形的性质得出即可.
解答: 解:(1)∵EF∥BC,
解:(1)∵EF∥BC,
∴△AEF∽△ABC,
∵AD⊥BC,
∴AD⊥EF,
∴
=
,
∵BC=4,AD=3,EF=x,
∴AG=GP=
x;
(2)如图1,2,当0<x≤2时,∵AG=
x,
∴y=
×x×
x=
x2,
如图3,当2<x<4时,
∵AG=GP=
x,AD=3,
∴DP=
x-3
∵EF∥BC,
∴△PMN∽△PEF,
∴
=
,
∴MN=2x-4,
∴y=S△PEF-S△PMN=
x2-
(
x-3)(2x-4)=-
x2+6x-6,
或∵EF∥BC,
∴△PMN∽△PEF,
∵AP⊥MN,EF,
∴
=(
)2,
而S△PEF=
x2,
∴S△PMN=
(
x-3)2=
x2-6x+6,
∴y=S△PEF-S△PMN=-
x2+6x-6.
 解:(1)∵EF∥BC,
解:(1)∵EF∥BC,∴△AEF∽△ABC,
∵AD⊥BC,
∴AD⊥EF,
∴
| AG |
| AD |
| EF |
| BC |
∵BC=4,AD=3,EF=x,
∴AG=GP=
| 3 |
| 4 |
(2)如图1,2,当0<x≤2时,∵AG=
| 3 |
| 4 |
∴y=
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
如图3,当2<x<4时,
∵AG=GP=
| 3 |
| 4 |
∴DP=
| 3 |
| 2 |
∵EF∥BC,
∴△PMN∽△PEF,
∴
| MN |
| EF |
| PD |
| PG |
∴MN=2x-4,
∴y=S△PEF-S△PMN=
| 3 |
| 8 |
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 8 |
或∵EF∥BC,
∴△PMN∽△PEF,
∵AP⊥MN,EF,
∴
| S△PMN |
| S△PEF |
| PD |
| PG |
而S△PEF=
| 3 |
| 8 |
∴S△PMN=
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
∴y=S△PEF-S△PMN=-
| 9 |
| 8 |
点评:此题主要考查了相似三角形的判定与性质以及三角形面积求法等知识,利用分类讨论得出是解题关键.

练习册系列答案
相关题目
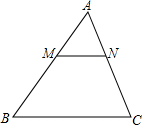 BCNM内的点A′,△A′MN与四边形BCNM重叠部分的面积为y.
BCNM内的点A′,△A′MN与四边形BCNM重叠部分的面积为y.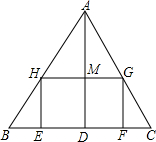 一个长HG是宽HE的2倍的矩形EFGH.使它的一边EF在BC上,顶点G,H分别在AC,AB上.AD与HG的交点为M.
一个长HG是宽HE的2倍的矩形EFGH.使它的一边EF在BC上,顶点G,H分别在AC,AB上.AD与HG的交点为M.