Question

【题目】如图1，矩形ABCD中，AB=4，AD=5，E为BC上一点，BE：CE=3：2，连接AE，点P从点A出发，沿射线AB的方向以每秒1个单位长度的速度匀速运动，过点P作PF∥BC交直线AE于点F．

（1）线段AE=　 　；

（2）设点P的运动时间为t（s），EF的长度为y，求y关于t的函数关系式，并写出t的取值范围；

（3）当t为何值时，以F为圆心的⊙F恰好与直线AB、BC都相切？并求此时⊙F的半径；

（4）如图2，将△AEC沿直线AE翻折，得到△AEC'，连结AC'，如果∠ABF=∠CBC′，求t值．（直接写出答案，不要求解答过程）．

Answer 1

【答案】（1）5；（2）y=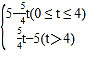；（3）12；（4）.

【解析】（1）由矩形性质知BC=AD=5，根据BE：CE=3：2知BE=3，利用勾股定理可得AE=5；

（2）由PF∥BE知，据此求得AF=t，再分0≤t≤4和t＞4两种情况分别求出EF即可得；

（3）由以点F为圆心的⊙F恰好与直线AB、BC相切时PF=PG，再分t=0或t=4、0＜t＜4、t＞4这三种情况分别求解可得；

（4）连接CC′，交直线AE于点Q，先证△CQE∽△ABE得，据此求得CQ=、CC′=2CQ=，再证△ABF∽△CBC′得，据此求得AF=，根据可得答案．

（1）∵四边形ABCD为矩形，

∴BC=AD=5，

∵BE：CE=3：2，

则BE=3、CE=2，

∴AE==5，

故答案为：5；

（2）如图1，当点P在线段AB上运动时，即0≤t≤4，

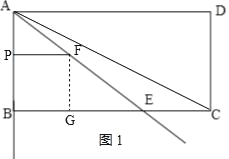
∵PF∥BE，

∴，即，

∴AF=，

则EF=AE﹣AF=5﹣，即y=5﹣ （0≤t≤4）；

如图2，当点P在射线AB上运动时，即t＞4，

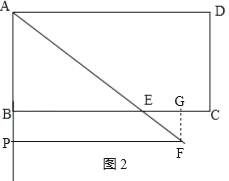
此时EF=AF﹣AE=﹣5，即y=﹣5 （t＞4）；

综上，y= ；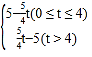

（3）以点F为圆心的⊙F恰好与直线AB、BC相切时，PF=PG，

分以下三种情况：①当t=0或t=4时，显然符合条件的⊙F不存在；

②当0＜t＜4时，如图1，作FG⊥BC于点G，

则FG=BP=4﹣t，

∵PF∥BC，

∴△APF∽△ABE，

∴，即，

∴PF=t，

由4﹣t=t可得t=，

则此时⊙F的半径PF=；

③当t＞4时，如图2，同理可得FG=t﹣4、PF=t，

由t﹣4=t可得t=16，

则此时⊙F的半径PF=12；

（4）如图3，连接CC′，交直线AE于点Q，

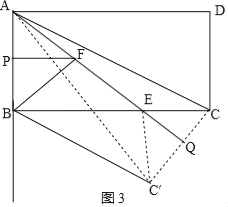
∵△CAQ≌△C′AQ，

∴AC=AC′、∠CAQ=∠C′AQ，

则∠CQE=∠ABE=90°，

∵∠CEQ=∠AEB，

∴△CQE∽△ABE，

∴，即，

∴CQ=，

则CC′=2CQ=，

∵∠ABF=∠CBC′、∠BAE=∠ECC′，

∴△ABF∽△CBC′，

∴，即，

解得： AF=，

由（2）知AF=t，

∴，

解得：t=．