题目内容
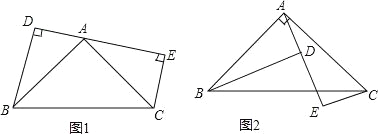
【题目】如图，在四边形ABCD中，对角线AC，BD交于点E，∠BAC=90°，∠CED=45°，∠DCE=30°，DE=
，BE=
．求CD的长和四边形ABCD的面积．
【答案】解：如图，过点D作DH⊥AC，
∵∠CED=45°，DH⊥EC，DE=
，∴EH=DH。
∵EH2+DH2=ED2，∴EH2=1。∴EH=DH=1。
又∵∠DCE=30°，∴CD=2，HC=
。
∵∠AEB=45°，∠BAC=90°，BE=
。∴AB=AE=2。
∴AC=2+1+
=3+
。
∴S四边形ABCD=
×2×（3+
）+
×1×（3+
）=
。
【解析】利用等腰直角三角形的性质得出EH=DH=1，进而得出再利用直角三角形中30°所对边等于斜边的一半得
出CD的长，求出AC，AB的长即可得出四边形ABCD的面积。
练习册系列答案
相关题目
