题目内容
5．解方程：（x2+x）2-4（x2+x）-12=0．分析 设y=x2+x，将原方程转化为关于y的一元二次方程，通过解方程求得y即x2+x的值，然后再来解关于x的一元二次方程．
解答 解：y=x2+x，则由原方程，得
y2-4y-12=0，
整理，得
（y-6）（y+2）=0，
解得y=6或y=-2，
当y=6时，x2+x=6，即（x+3）（x-2）=0，
解得x1=-3，x2=2．
当y=-2时，x2+x=-2，即x2+x+2=0，该方程无解．
综上所述，该方程的解为：x1=-3，x2=2．
点评 本题主要考查了换元法，即把某个式子看作一个整体，用一个字母去代替它，实行等量替换．
练习册系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
相关题目
15．
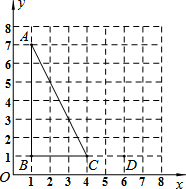如图，点A，B，C，D的坐标分别是（1，7），（1，1），（4，1），（6，1），以C，D，E为顶点的三角形与△ABC相似，则点E的坐标不可能是（ ）
如图，点A，B，C，D的坐标分别是（1，7），（1，1），（4，1），（6，1），以C，D，E为顶点的三角形与△ABC相似，则点E的坐标不可能是（ ）| A． | （4，0） | B． | （6，2） | C． | （6，3） | D． | （4，5） |
由几个大小不同的正方形组成的几何图形如图，则它的主视图是（ ）
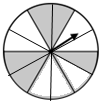如图，一个圆形转盘被分成12个圆心角都为30°的扇形，任意转动这个转盘1次，当转盘停止转动时，指针指向阴影区域的概率是$\frac{5}{12}$．
如图，一次函数y=kx+2的图形与反比例函数y=$\frac{m}{x}$的图象交于点P，点P在第一象限，PA⊥x轴于点A，一次函数的图象分别交x轴、y轴于点C、D，且S△COD=1，$\frac{CO}{OA}=\frac{1}{2}$．