Question

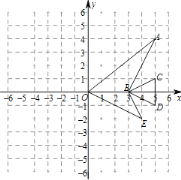
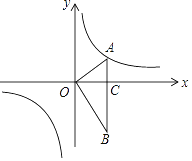
【题目】如图，OA⊥OB，AB⊥x轴于C，点A（，1）在反比例函数y=的图象上．

（1）求反比例函数y=的表达式；

（2）在x轴上存在一点P，使S△AOP= S△AOB， 求点P的坐标．

Answer 1

【答案】（1）；（2）（﹣2，0），或（2，0）

【解析】试题分析：（1）把A的坐标代入反比例函数的解析式，即可求出答案；

（2）求出∠A＝60°，∠B＝30°，求出线段OA和OB，求出△AOB的面积，根据已知S△AOP＝S△AOB，求出OP长，即可求出答案．

试题解析：

（1）解：把A（ ，1）代入反比例函数y＝ 得：k＝1× ＝ ，

所以反比例函数的表达式为y＝ ；

（2）解：∵A（ ，1），OA⊥AB，AB⊥x轴于C，

∴OC＝ ，AC＝1，

OA＝ ＝ ＝2，

∵tanA＝ ＝ ，

∴∠A＝60°，

∵OA⊥OB，

∴∠AOB＝90°，

∴∠B＝30°，

∴OB＝2OC﹣2 ，

∴S△AOB＝ ＝ ＝2 ，

∵S△AOP＝ S△AOB ，

∴ ，

∵AC＝1，∴OP＝2 ，

∴点P的坐标为（﹣2 ，0），或（2 ，0）．