题目内容
如图,在直角坐标系中,已知点A(2,0),B(0,4),在坐标轴上找到点C(1,0)和点D,使△AOB
与△DOC相似,求出D点的坐标,并说明理由.
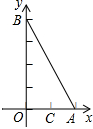
与△DOC相似,求出D点的坐标,并说明理由.
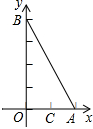
(0,
)或(0,-
)或(0,2)或(0,-2).
理由:若△AOB与△DOC相似,点D在x轴上方:
∠B=∠OCD,∴
=
,即
=
,∴D(0,
),
同理,点D在x轴下方:D(0,-
).
若△AOB与△COD相似,点D在x轴上方:可得D(0,2);
若△AOB与△COD相似,点D在x轴下方:可得D(0,-2).
| 1 |
| 2 |
| 1 |
| 2 |
理由:若△AOB与△DOC相似,点D在x轴上方:
∠B=∠OCD,∴
| OC |
| OB |
| OD |
| OA |
| 1 |
| 4 |
| OD |
| 2 |
| 1 |
| 2 |
同理,点D在x轴下方:D(0,-
| 1 |
| 2 |
若△AOB与△COD相似,点D在x轴上方:可得D(0,2);
若△AOB与△COD相似,点D在x轴下方:可得D(0,-2).

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目