题目内容
已知△ABC的三个内角满足3∠A>5∠B,3∠C≤2∠B.请找出3组符合条件的∠A、∠B、∠C的度数,再判断此三角形的形状并说明理由.
考点:三角形内角和定理
专题:
分析:都取等号用∠B表示出∠A、∠C,再根据三角形的内角和等于180°列方程求出∠B,然后表示出最大的角∠A,从而求出∠A的范围,然后分别写出即可.
解答:解:设3∠A=5∠B,3∠C=2∠B,
则∠A=
∠B,∠C=
∠B,
∵∠A+∠B+∠C=180°,
∴
∠B+∠B+
∠B=180°,
解得∠B=54°,
∵3∠A>5∠B,
∴最大的角∠A>54°×
=90°,
∴三组符合条件的度数分别为100°,50°,30°,110°,50°,20°,120°,40°,20°.
则∠A=
| 5 |
| 3 |
| 2 |
| 3 |
∵∠A+∠B+∠C=180°,
∴
| 5 |
| 3 |
| 2 |
| 3 |
解得∠B=54°,
∵3∠A>5∠B,
∴最大的角∠A>54°×
| 5 |
| 3 |
∴三组符合条件的度数分别为100°,50°,30°,110°,50°,20°,120°,40°,20°.
点评:本题考查了三角形内角和定理,取等号并求出最大的内角的度数大于90°是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个扇形的周长为8m,则它的最大面积是( )
| A、4m2 |
| B、6m2 |
| C、8m2 |
| D、10m2 |
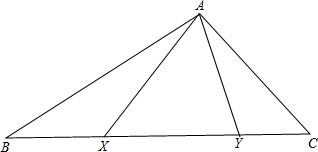 如图,自△ABC的顶点A引两条射线交BC于X,Y,使得∠BAX=∠CAY,求证:
如图,自△ABC的顶点A引两条射线交BC于X,Y,使得∠BAX=∠CAY,求证: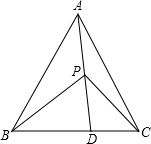 如图所示,在△ABC中,AB=AC,BD=2DC,P在AD上,∠BAC=∠BPD,求证:∠BPD=2∠CPD.
如图所示,在△ABC中,AB=AC,BD=2DC,P在AD上,∠BAC=∠BPD,求证:∠BPD=2∠CPD.