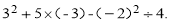题目内容
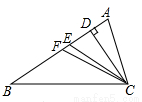
(本题满分10分) 如图,在△ABC中,点E、G分别在BC、AC上,CD⊥AB,EF⊥AB,垂足分别为D、F.已知∠1+∠2=180°,∠3=105°,求∠ACB的度数.请将求∠ACB度数的过程填写完整.
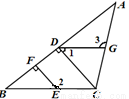
【解析】
∵EF⊥AB,CD⊥AB,(已知)
∴∠BFE=90°,∠BDC=90°,
理由是: .
∴∠BFE=∠BDC,
∴EF∥CD,理由是: .
∴ ∠2+∠ =180°,理由是: .
又∵ ∠1 +∠2=180°(已知),
∴ ∠1 = .
∴ BC∥ ,理由是: .
∴∠3 = ,理由是: .
又∵∠3 = 105°(已知),
∴∠ACB= .
(垂直的定义),(同位角相等,两直线平行),∠BCD,(两直线平行,同旁内角互补),∠BCD,DG,(内错角相等,两直线平行),∠ACB,(两直线平行,同位角相等),105°
【解析】
试题分析:根据垂直的定义可得∠BFE=∠BDC=90°,然后根据同位角相等,两直线平行可得CD∥EF,再根据两直线平行,同位角相等可得∠2=∠BCD,然后求出∠1=∠BCD,再根据内错角相等,两直线平行,然后根据两直线平行,同位角相等可得∠3=∠ACB.
试题解析:∵EF⊥AB,CD⊥AB,(已知)
∴∠BFE=90°,∠BDC=90°,(垂直的定义).
∴∠BFE=∠BDC,
∴EF∥CD,(同位角相等,两直线平行).
∴ ∠2+∠BCD=180°,(两直线平行,同旁内角互补).
又∵ ∠1 +∠2=180°(已知),
∴ ∠1 = ∠BCD.
∴ BC∥ DG,(内错角相等,两直线平行).
∴∠3 = ∠ACB ,(两直线平行,同位角相等).
又∵∠3 = 105°(已知)
∴∠ACB= 105°
考点:平行线的性质和判定.

 的顶点都在格点上,点A的坐标为(-3,2)。请按要求分别完成下列各小题:
的顶点都在格点上,点A的坐标为(-3,2)。请按要求分别完成下列各小题: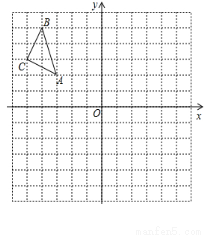
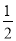 ∠ACB D.CD⊥BE
∠ACB D.CD⊥BE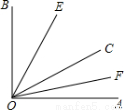
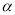 ,求∠EOF的度数(写出求解过程);
,求∠EOF的度数(写出求解过程);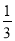 ∠COB,∠COF=
∠COB,∠COF=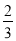 ∠COA”,且∠AOB=
∠COA”,且∠AOB=