题目内容
一次函数 分别交x轴、y轴于A、B两点,在x轴上取一点,使△ABC为等腰三角形,则这样的的点C最多有 个
分别交x轴、y轴于A、B两点,在x轴上取一点,使△ABC为等腰三角形,则这样的的点C最多有 个
4
解析试题考查知识点:函数、直角坐标系、等腰三角形、作图
思路分析:确定A、B两点,再分别以AB为底、腰推断满足条件的三角形的C点的位置
具体解答过程:
如图所示。
对于一次函数 ,令x=0得y=4;令y=0得x=-3,故知函数与x轴交点为A(-3,0)与y轴交点为B(0,4),且AB=5。要在x轴上取一点,使△ABC为等腰三角形,则:
,令x=0得y=4;令y=0得x=-3,故知函数与x轴交点为A(-3,0)与y轴交点为B(0,4),且AB=5。要在x轴上取一点,使△ABC为等腰三角形,则:
(1)、如下图所示。当以线段AB为底时,做线段AB的垂直平分线,交x轴于C1,则△ABC1必为等腰三角形;
(2)、如下图所示。当以线段AB为腰时,在OA的延长线上截取长度为5的线段AC2,交x轴于C2,则△ABC2必为等腰三角形;
(3)、如下图所示。当以线段AB为腰时,在AO的延长线上找到一点C3,使AC3长度为5的线段AC3,交x轴于C3,则△ABC3必为等腰三角形;
(4)、如下图所示。当以线段AB为腰时,在x轴正半轴上找到A点的对称点C4,使线段OA=OC4= 3,则△ABC4必为等腰三角形;
综上所述,符合条件的C点最多能找到4个。
试题点评:这道题目虽是个填空题,但要细作起来,还是较为费事的。不过对于培养空间想象能力来说,这道题目还是上乘之作。

练习册系列答案
相关题目
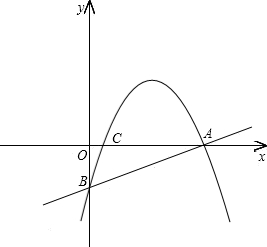

 分别交x轴,y轴于A,B两点,在x轴上取一点,使△ABC为等腰三角形,则这样的点C最多有_____个。
分别交x轴,y轴于A,B两点,在x轴上取一点,使△ABC为等腰三角形,则这样的点C最多有_____个。 分别交y轴、x轴于A、B两点,抛物线y=-x2+bx+c过A、B两点.
分别交y轴、x轴于A、B两点,抛物线y=-x2+bx+c过A、B两点.
 分别交x轴、y轴于A、B两点,在x轴上取一点,
分别交x轴、y轴于A、B两点,在x轴上取一点,