题目内容
一次函数 分别交x轴,y轴于A,B两点,在x轴上取一点,使△ABC为等腰三角形,则这样的点C最多有_____个。
分别交x轴,y轴于A,B两点,在x轴上取一点,使△ABC为等腰三角形,则这样的点C最多有_____个。
4
解析试题分析:首先求出A,B的坐标,由△ABC为等腰三角形,根据顶点C的确定方法即可求解.
在 中,令y=0,解得x=-3;令x=0,解得y=4
中,令y=0,解得x=-3;令x=0,解得y=4
则直线与x轴、y轴的交点A、B分别是(-3,0),(0,4)
当AB是底边时,顶点C是线段AB的垂直平分线与x轴的交点
当AB是腰时,分两种情况:
(1)当A是顶角的顶点时,第三个顶点C,就是以A为圆心,以AB为半径的圆与x轴的交点,有2个
(2)当B是顶角的顶点时,第三个顶点C,就是以B为圆心,以AB为半径的圆与x轴的交点,有1个
故这样的点C最多有4个.
考点:等腰三角形的性质
点评:解答本题的关键是要对三角形进行分类讨论,同学们要注意不能漏掉其中的任一解.

练习册系列答案
相关题目
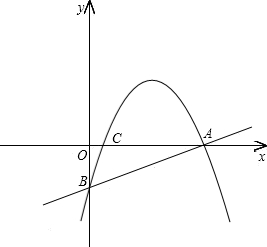

 分别交y轴、x轴于A、B两点,抛物线y=-x2+bx+c过A、B两点.
分别交y轴、x轴于A、B两点,抛物线y=-x2+bx+c过A、B两点.
 分别交x轴、y轴于A、B两点,在x轴上取一点,
分别交x轴、y轴于A、B两点,在x轴上取一点,