Question

【题目】(1)如图，在等腰直角中，，，将边绕点顺时针旋转得到线段，则的面积为_______．

(2)如图,在直角 中，，，将边绕点顺时针旋转得到线段，连接，求的面积，并说明理由．（用含的式子表示）

(3)如图，在等腰中，，将边绕点顺时针旋转得到线段，连接，若，则 的面积为 （用含的式子表示）.

Answer 1

【答案】（1）18；（2）；理由见解析；（3）

【解析】

（1）首先连接AD，根据等腰直角三角形的性质得出∠CAB=∠CBA=45°，然后根据AB=BD，∠ABD=90°，得出∠BAD=∠BDA=45°，进而得出∠CBA=∠BAD，内错角相等，得出AD∥BC，进而得出△BCD的高即为AC，即可得出面积；

（2）首先过D作CB边上的高DG交CB的延长线于G，根据∠ACB=∠ABD=90°进行等角转换，得出∠ABC=∠BDG，∠A=∠DBG，即可判定△ABC≌△DBG（ASA），得出BC=DG，进而得出面积；

（3）首先作AE⊥BC于E，根据等腰三角形三线合一的性质，得出CE=BE=，依据（2）中的方法同理可得△ABE≌△BDF，得出△BCD的高即为EB，即可求得面积.

（1）连接AD，如图所示

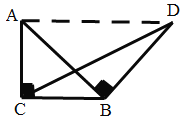
∵等腰直角，

∴∠CAB=∠CBA=45°

又∵AB=BD，∠ABD=90°

∴∠BAD=∠BDA=45°

∴∠CBA=∠BAD

∴AD∥BC

∴△BCD的高即为AC

∴

（2）过D作CB边上的高DG交CB的延长线于G，如图所示

∵∠ACB=∠ABD=90°

∴∠ABC+∠A=∠ABC+∠DBG=∠DBG+∠BDG

∴∠ABC=∠BDG，∠A=∠DBG

又∵AB=BD

∴△ABC≌△DBG（ASA）

∴BC=DG

∴

（3）作AE⊥BC于E，DF⊥CB，交CB的延长线于F，如图所示

∵等腰中，，

∴CE=BE=

由（2），同理可得，△ABE≌△BDF

△BCD的高即为EB