Question

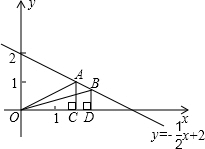如图，一次函数y=-

1

2

x+2的图象上有两点A、B，A点的横坐标为2，B点的横坐标为a（0＜a＜4且a≠2），过点A、B分别作x的垂线，垂足为C、D，△AOC、△BOD的面积分别为S₁、S₂，则S₁、S₂的大小关系是（　　）

• A、S₁＞S₂
• B、S₁=S₂
• C、S₁＜S₂
• D、无法确定

Answer 1

分析：△AOC的面积S₁已知，△BOD的面积S₂可由关于a的函数表示，求出S₂的取值范围，跟S₁比较即可．

解答：解：由一次函数图象可得出A（2，1），
则S₁=

1

2

×2×1=1，
S₂=

1

2

×a×(-

1

2

a+2)=-

1

4

(a-2)2+1
又0＜a＜4且a≠2，
∴S₂＜1=S₁，
故此题选A

点评：本题考查的是由一次函数确定坐标，根据坐标表示出面积并比较大小，另外还考查了二次函数的性质．