题目内容
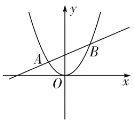
【题目】如图，一次函数
与抛物线
交于A，B两点，且点A的横坐标是
，点B的横坐标是3，则以下结论：①抛物线的图象的顶点一定是原点；②
时，一次函数与抛物线的函数值都随x的增大而增大；③
的长度可以等于5；④当
时，
.其中正确的结论是（ ）
A.①②③B.①②④C.①③④D.①②③④
【答案】B
【解析】
①由顶点坐标公式判断即可；
②根据图象得到一次函数y=kx+b为增函数，抛物线当x大于0时为增函数，本选项正确；
③AB长不可能为5，由A、B的横坐标求出AB为5时，直线AB与x轴平行，即k=0，与已知矛盾；
④直线y=-kx+b与y=kx+b关于y轴对称，作出对称后的图象，故y=-kx+b与抛物线交点横坐标分别为-3与2，找出一次函数图象在抛物线上方时x的范围判断即可．
解：①抛物线
，利用顶点坐标公式得顶点坐标为
，正确.
②由题图可知，在y轴右侧，即当
时，一次函数与抛物线的函数值都随x的增大而增大，正确.
③如解图，过点A作x轴的平行线，过点B作y轴的平行线，两线相交于点D.在
中，由A、B横坐标分别为
，3，可知
，故
，错误.
④直线
与
关于y轴对称，如解图所示，可得出直线与抛物线交点E、F横坐标分别为
，2，由解图可知当
时，
，即
，正确.
综上所述，正确的结论有①②④.
练习册系列答案
相关题目
