题目内容
如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度向B点运动,同时动点N自A点出发沿折线AD﹣DC﹣CB以每秒3cm的速度运动,到达B点时运动同时停止.设△AMN的面积为y(cm2),运动时间为x(秒),则下列图象中能大致反映y与x之间的函数关系的是( )


A.
 B.
B.
 C.
C.
 D.
D.

B【考点】动点问题的函数图象.
【分析】当点N在AD上时,易得S△AMN的关系式;当点N在CD上时,高不变,但底边在增大,所以S△AMN的面积关系式为一个一次函数;当N在BC上时,表示出S△AMN的关系式,根据开口方向判断出相应的图象即可.
【解答】解:当点N在AD上时,即0≤x≤1,S△AMN=
 ×x×3x=
×x×3x=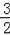
 x2,
x2,
点N在CD上时,即1≤x≤2,S△AMN=
 ×x×3=
×x×3=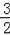
 x,y随x的增大而增大,所以排除A、D;
x,y随x的增大而增大,所以排除A、D;
当N在BC上时,即2≤x≤3,S△AMN=
 ×x×(9﹣3x)=﹣
×x×(9﹣3x)=﹣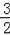
 x2+
x2+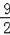
 x,开口方向向下.
x,开口方向向下.
故选:B
【点评】此题考查动点问题的函数图象问题,根据自变量不同的取值范围得到相应的函数关系式是解决本题的关键.

 阅读快车系列答案
阅读快车系列答案随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为2000元、1700元的A、B两种型号的净水器,下表是近两周的销售情况:
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 18000元 |
| 第二周 | 4台 | 10台 | 31000元 |
(1)求A,B两种型号的净水器的销售单价;
(2)若电器公司准备用不多于54000元的金额在采购这两种型号的净水器共30台,求A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这30台净水器能否实现利润为12800元的目标?若能,请给出相应的采购方案;若不能,请说明理由.

 的平方根是
的平方根是 


 的解,则直线l的图象不经过( )
的解,则直线l的图象不经过( )
 x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.
x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.


 B.
B.
 C.
C.
 D.
D.


 (k≠0,x>0)的图象过点B,E.若AB=4,则k的值为 .
(k≠0,x>0)的图象过点B,E.若AB=4,则k的值为 .
