Question

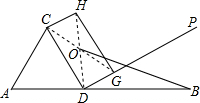如图，线段AB的长为20

2

cm，点D在AB上，点AD上的△ACD是边长为10cm的等边三角形，过点D作与CD垂直的射线DP，过DP上一动点G（不与D重合）作矩形CDGH，记矩形CDGH的对角线交点为O，连接OB，则线段BO的最小值为

10

2

cm

．

Answer 1

分析：连接CG、HD．根据矩形的对角线互相平分、相等的性质推知CO=DO；然后由等腰△COD和等边△ACD的性质推知AO垂直平分CD；最后确定点B的位置为直角△AOB的一直角边，根据含30°角的直角三角形的性质求OB的长度即可．

解答：解：连接CG、HD．
∵四边形CDGH是矩形，CG、HD交于点O，
∴CO=DO；
又∵AC=AD，
∴AO⊥CD，且AO平分CD；
∴BO的最小值是点B到CD的中垂线的距离；
∴△AOB是直角三角形，
∴BO=

1

2

AB=10

2

（30°所对的直角边是斜边的一半）．
故答案是：10

2

cm．

点评：本题考查了等边三角形的性质、线段垂直平分线的性质以及矩形的性质．解答此题的关键是确定点B的位置．