题目内容
如图，为了测量一个大峡谷的宽度，地质勘探人员在对面的岩石上观察到一个特别明显的标志点O，再在他们所在的这一侧选点A，B，D，使AB⊥AO，DB⊥AB，然后确定DO和AB的交点C，测得AC=120m，CB=60m，BD=50m，请你帮助他们算出峡谷的宽AO．
解：如图，∵AB⊥AO，DB⊥AB，
∴∠A=∠B=90°，
又∠ACO=∠BCD（对顶角相等），
∴△ACO∽△BCD，
∴
=
，
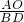∵AC=120m，CB=60m，BD=50m，
∴
=
，
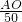解得AO=2×50=100m，
即峡谷的宽AO是100m．
分析：先确定△ACO与△BCD相似，再根据相似三角形对应边成比例列出比例式即可求出AO的宽度．
点评：本题主要考查了相似三角形的应用，利用了相似三角形对应边成比例的性质，构造出相似三角形是解题的关键．
∴∠A=∠B=90°，
又∠ACO=∠BCD（对顶角相等），
∴△ACO∽△BCD，
∴
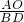=，∵AC=120m，CB=60m，BD=50m，
∴
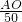=，解得AO=2×50=100m，
即峡谷的宽AO是100m．
分析：先确定△ACO与△BCD相似，再根据相似三角形对应边成比例列出比例式即可求出AO的宽度．
点评：本题主要考查了相似三角形的应用，利用了相似三角形对应边成比例的性质，构造出相似三角形是解题的关键．
练习册系列答案
相关题目
21、如图，小华家的住宅楼AB与北京奥运会主体育场鸟巢隔水相望且能看到鸟巢的最高处CD，两建筑物的底部在同一水平面上，视野开阔，但不能直接到达，小华为了测量鸟巢的最大高度CD，只能利用所在住宅楼的地理位置．现在小华仅有的测量工具是皮尺和测角仪（皮尺可测量长度，测角仪可测量仰角、俯角），请你帮助小华设计一个测量鸟巢的最大高度的方案．
近几年，大伊山风景区的建设成果显著，建成了石佛寺和大佛．大佛是当今世界上最大的坐佛，他华贵雍容、面慈目善、金光闪烁，成为灌云一个地标，招徕游客一大亮点．那么，他到底有多高呢？如图，为了测量他的高度，先在地面上用测角仪自A处测得她的顶部的仰角是30°，然后在水平地面上向他前进了70m，此时自B处测得他的顶部的仰角是45°．已知测角仪的高度是1.5m，请你计算出他的高度．（取
为了给市民提供一个休闲健身的场所，市政府决定将一块矩形（如图）空地规划成休闲广场，初步规划AB为1200米，BC长为400米，后经测量发现，如果AB长每减少30米，则BC长就可增加20米，为了合理的利用土地，AB长又不能小于600米，设AB边的长为x米．矩形休闲广场的占地面积为S平方米．
近几年，大伊山风景区的建设成果显著，建成了石佛寺和大佛．大佛是当今世界上最大的坐佛，他华贵雍容、面慈目善、金光闪烁，成为灌云一个地标，招徕游客一大亮点．那么，他到底有多高呢？如图，为了测量他的高度，先在地面上用测角仪自A处测得她的顶部的仰角是30°，然后在水平地面上向他前进了70m，此时自B处测得他的顶部的仰角是45°．已知测角仪的高度是1.5m，请你计算出他的高度．（取
=1.732，结果精确到1m）