题目内容
12.已知直线y=2x+2与两坐标轴交于A,B两点,过B作AB的垂线交x轴于点C,求经过点A,B,C的抛物线的函数表达式.分析 根据直线的解析式求得A、B的坐标,从而求得OA=1,OB=2,然后根据OB2=OA•OC得出OC=4,从而得出C(4,0),最后根据待定系数法即可求得.
解答 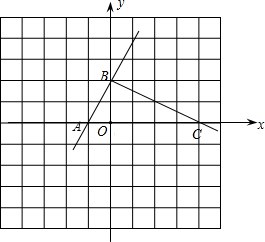 解:由直线y=2x+2可知A(-1,0),B(0,2),
解:由直线y=2x+2可知A(-1,0),B(0,2),
∵AB⊥BC,
∴OB2=OA•OC,即22=1×OC,
解得OC=4,
∴C(4,0),
设抛物线的解析式为y=ax2+bx+c,
∴$\left\{\begin{array}{l}{a-b+c=0}\\{c=2}\\{16a+4b+c=0}\end{array}\right.$
解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=\frac{3}{2}}\\{c=2}\end{array}\right.$,
∴经过点A,B,C的抛物线的函数表达式为y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2.
点评 本题考查了待定系数法求二次函数的解析式,射影定理的应用等,熟练掌握待定系数法是解题的关键.

练习册系列答案
相关题目
17.同时满足不等式y>-1和y<2的整数有多少个?( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
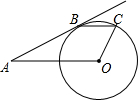 如图,AB切⊙O于点B,OA=5$\sqrt{5}$,tanA=$\frac{1}{2}$,弦BC∥OA
如图,AB切⊙O于点B,OA=5$\sqrt{5}$,tanA=$\frac{1}{2}$,弦BC∥OA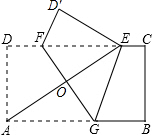 如图,已知矩形纸片ABCD,AD=2,AB=4,将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB,CD交于点G、F、AE与FG交于点O.求证:A,G,E,F四点围成的四边形是菱形.
如图,已知矩形纸片ABCD,AD=2,AB=4,将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB,CD交于点G、F、AE与FG交于点O.求证:A,G,E,F四点围成的四边形是菱形.