题目内容
如图1,△ABC和△BCD中,∠ABC=∠DCB=90°,AB=3,BC=4,CD=5,AC与BD交于点E,点P从点C出发,以每秒1个单位的速度沿CA向点A运动.过点P作PQ∥CD,交BD于Q点,以PQ为边向右作正方形PQMN,设点P的运动时间为x(秒).(1)CE=______;当PQ=
 时,x=______;
时,x=______;(2)当点P在线段CE上运动时,设线段PQ的长为y,求y与x之间的函数关系式;
(3)当点P在线段CE上运动时,设正方形PQMN与△ECD重叠部分(阴影部分)的面积为S(平方单位),求S与x之间的函数关系式;当x为何值时,S有最大值?
(4)当0≤x≤5时,直接写出AC的中点在正方形PQMN内部时x的取值范围.

【答案】分析:(1)根据AB∥CD,可以得到 =
= ,即可求得CE的长度,进而依据PQ∥CD,得到
,即可求得CE的长度,进而依据PQ∥CD,得到 =
= 求得EP的长,进而得到CP的长度,求得x的值;
求得EP的长,进而得到CP的长度,求得x的值;
(2)根据PQ∥CD,得到△EQP∽△EDC,在根据相似三角形的对应边的比相等即可求得函数的解析式;
(3)根据△EQP∽△EDC,利用x表示出PN的长,则函数解析式即可求得,然后利用二次函数的性质,即可求得最值;
(4)显然,当P在CE上时,不合题意.则P一定在AE上,根据AC的中点O到PQ的距离一定小于正方形的边长,即可求得x的范围.
解答:解:(1)在直角△ABC中,AC= =5,
=5,
∵∠ABC=∠DCB=90°
∴AB∥CD
∴ =
= =
=
∴CE= ,
,
∵PQ∥CD
∴ =
= =
= =
= ,
,
∴PE= CE=
CE=
∴x=CP=EC-EP= ,
,
当点P在EA上时,也可能出现PQ=2.5,此时x= ;
;
(2)∵PQ∥CD,
∴△EQP∽△EDC.
∴ =
=
∴ =
=
∴y=- x+5;
x+5;
(3)设PN与CD的交点为K,由△CKP∽△ABC得 ,
,
应分两种情况讨论:①0≤x≤ 时,S=-
时,S=- x2+4x,
x2+4x,
当x= 时,S有最大值为
时,S有最大值为 ;
;
②当 时,
时, ,
,
对应图象在对称轴左侧,此时S随x的增大而减小,当 时,S有最大值
时,S有最大值 .
.
综上所述,当x= 时,S有最大值为
时,S有最大值为 ;
;
(4)显然,当P在CE上时,不合题意.当P在AE上时,PQ= -5,
-5,
设AC中点为O,O到PQ的距离为OT,则OT= -2,
-2,
由PQ>OT即 -5>
-5> -2,得x>
-2,得x> .
.
所以 <x≤5为所求.
<x≤5为所求.
点评:本题考查了相似三角形的判定与性质与二次函数的性质的综合应用,正确求得函数的解析式是关键.
 =
= ,即可求得CE的长度,进而依据PQ∥CD,得到
,即可求得CE的长度,进而依据PQ∥CD,得到 =
= 求得EP的长,进而得到CP的长度,求得x的值;
求得EP的长,进而得到CP的长度,求得x的值;(2)根据PQ∥CD,得到△EQP∽△EDC,在根据相似三角形的对应边的比相等即可求得函数的解析式;
(3)根据△EQP∽△EDC,利用x表示出PN的长,则函数解析式即可求得,然后利用二次函数的性质,即可求得最值;
(4)显然,当P在CE上时,不合题意.则P一定在AE上,根据AC的中点O到PQ的距离一定小于正方形的边长,即可求得x的范围.
解答:解:(1)在直角△ABC中,AC=
 =5,
=5,∵∠ABC=∠DCB=90°
∴AB∥CD
∴
 =
= =
=
∴CE=
 ,
,∵PQ∥CD
∴
 =
= =
= =
= ,
,∴PE=
 CE=
CE=
∴x=CP=EC-EP=
 ,
,当点P在EA上时,也可能出现PQ=2.5,此时x=
 ;
;(2)∵PQ∥CD,
∴△EQP∽△EDC.
∴
 =
=
∴
 =
=
∴y=-
 x+5;
x+5;(3)设PN与CD的交点为K,由△CKP∽△ABC得
 ,
,应分两种情况讨论:①0≤x≤
 时,S=-
时,S=- x2+4x,
x2+4x,当x=
 时,S有最大值为
时,S有最大值为 ;
; ②当
 时,
时, ,
,对应图象在对称轴左侧,此时S随x的增大而减小,当
 时,S有最大值
时,S有最大值 .
.综上所述,当x=
 时,S有最大值为
时,S有最大值为 ;
; (4)显然,当P在CE上时,不合题意.当P在AE上时,PQ=
 -5,
-5,设AC中点为O,O到PQ的距离为OT,则OT=
 -2,
-2,由PQ>OT即
 -5>
-5> -2,得x>
-2,得x> .
.所以
 <x≤5为所求.
<x≤5为所求.点评:本题考查了相似三角形的判定与性质与二次函数的性质的综合应用,正确求得函数的解析式是关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 15、如图,在△ABC和△DEF中,已知AB=DE,AC=DF,要使△ABC≌△DEF,根据三角形全等的判定公理还需添加条件(填上你认为正确的一种情况)
15、如图,在△ABC和△DEF中,已知AB=DE,AC=DF,要使△ABC≌△DEF,根据三角形全等的判定公理还需添加条件(填上你认为正确的一种情况)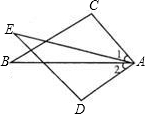 如图:在△ABC和△ADE中,已知∠1=∠2,∠B=∠E,AC=AD.请说明△ABC≌△AED的理由.
如图:在△ABC和△ADE中,已知∠1=∠2,∠B=∠E,AC=AD.请说明△ABC≌△AED的理由.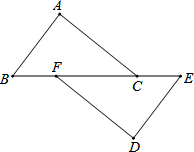 (2013•上海)如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,BF=CE,AC∥DF,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是
(2013•上海)如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,BF=CE,AC∥DF,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是 如图,在△ABC和△ADE中,∠DAB=∠EAC,∠C=∠E.
如图,在△ABC和△ADE中,∠DAB=∠EAC,∠C=∠E. 如图,在△ABC和△EFD中,AB=EF,AC=ED,点B,D,C,F在一条直线上.
如图,在△ABC和△EFD中,AB=EF,AC=ED,点B,D,C,F在一条直线上.