题目内容
 梯形ABCD是由三个直角三角形拼成的,各直角边的长度如图.
梯形ABCD是由三个直角三角形拼成的,各直角边的长度如图.(1)请你运用两种方法计算梯形ABCD的面积;
(2)根据(1)的计算,探索a、b、c三者之间的关系,并用式子表示出来.
分析:(1)利用梯形面积公式求出梯形面积;由三个三角形面积之和求出梯形面积;
(2)根据两种求法得出的面积相等列出关系式,化简即可得到结果.
(2)根据两种求法得出的面积相等列出关系式,化简即可得到结果.
解答:解:(1)梯形面积为
;也可以为
ab+
ab+
c2;
(2)根据(1)得:
=
ab+
ab+
c2,
去分母得:a2+2ab+b2=2ab+c2,即a2+b2=c2.
| (a+b)(a+b) |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据(1)得:
| (a+b)(a+b) |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
去分母得:a2+2ab+b2=2ab+c2,即a2+b2=c2.
点评:此题考查了整式的混合运算,以及勾股定理的证明,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
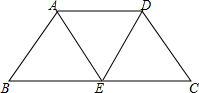 如图,已知等腰梯形ABCD是由三个边长为2的全等的正三角形围成的,则等腰梯形ABCD的面积是
如图,已知等腰梯形ABCD是由三个边长为2的全等的正三角形围成的,则等腰梯形ABCD的面积是
 如图,已知等腰梯形ABCD是由三个边长为2的全等的正三角形围成的,则等腰梯形ABCD的面积是________.
如图,已知等腰梯形ABCD是由三个边长为2的全等的正三角形围成的,则等腰梯形ABCD的面积是________.