题目内容
 将长为12,宽为5的矩形纸片沿对角线对折后放在桌面上,那么它覆盖的桌面的面积等于________.
将长为12,宽为5的矩形纸片沿对角线对折后放在桌面上,那么它覆盖的桌面的面积等于________.
42
分析:设长方形ABCD沿AC对折后AD交BC于E,过E作EF⊥AC于F,由△AFE∽△ADC,可得EF=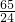 ,即可计算折叠后的面积,即可解题.
,即可计算折叠后的面积,即可解题.
解答: 解:如图,设长方形ABCD沿AC对折后AD交BC于E,过E作EF⊥AC于F,
解:如图,设长方形ABCD沿AC对折后AD交BC于E,过E作EF⊥AC于F,
因为∠1=∠2=∠3,则有AE=CE,故AF=FC= ,
,
由△AFE∽△ADC,则EF=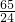 ,
,
所以折叠后面积=S长方形ABCD-S△AEC,
=5×12- ×13×
×13×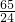 ,
,
=42 .
.
故答案为:42 .
.
点评:本题考查了三角形面积的计算,三角形相似的判定,相似三角形对应边比值相等的性质,本题中求△AEC的面积是解题的关键.

分析:设长方形ABCD沿AC对折后AD交BC于E,过E作EF⊥AC于F,由△AFE∽△ADC,可得EF=
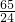 ,即可计算折叠后的面积,即可解题.
,即可计算折叠后的面积,即可解题.解答:
 解:如图,设长方形ABCD沿AC对折后AD交BC于E,过E作EF⊥AC于F,
解:如图,设长方形ABCD沿AC对折后AD交BC于E,过E作EF⊥AC于F,因为∠1=∠2=∠3,则有AE=CE,故AF=FC=
 ,
,由△AFE∽△ADC,则EF=
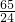 ,
,所以折叠后面积=S长方形ABCD-S△AEC,
=5×12-
 ×13×
×13×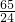 ,
,=42
 .
.故答案为:42
 .
.点评:本题考查了三角形面积的计算,三角形相似的判定,相似三角形对应边比值相等的性质,本题中求△AEC的面积是解题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
