Question

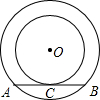
如图，⊙O的半径OC为6cm，弦AB垂直平分OC，则AB=______cm，∠AOB=______．

Answer 1

设OC与AB的交点为D，如图所示：

∵半径OC⊥AB，
∴点D为弦AB的中点，即AD=BD=

1

2

AB，
又∵弦AB垂直平分OC，且OC=6cm，
∴OD=CD=

1

2

OC=3cm，
在Rt△AOD中，OA=OC=6cm，OD=3cm，
根据勾股定理得：AD=

OA2-OD2

=3

3

cm，
则AB=2AD=6

3

cm，
∵OA=OB，OD⊥AB，
∴OC为∠AOB的平分线，即∠AOC=∠BOC=

1

2

∠AOB，
在Rt△AOD中，sin∠AOC=

AD

OA

=

3 3

6

=

3

2

，
∴∠AOC=60°，
则∠AOB=2∠AOC=120°．
故答案为：6

3

；120°