Question

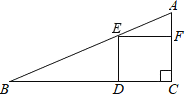
【题目】如图，在平行四边形中，、相交于点，点是的中点，连接并延长交于点，，则下列结论：①；②；③；④，其中一定正确的是(　　)．

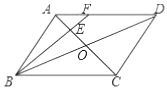
A.①②③④B.①②C.②③④D.①②③

Answer 1

【答案】D

【解析】

①根据平行四边形的性质可得出CE＝3AE，由AF∥BC可得出△AEF∽△CEB，根据相似三角形的性质可得出BC＝3AF，进而可得出DF＝2AF，结论①正确；

②根据相似三角形的性质结合S△AEF＝4，即可求出S△BCE＝9S△AEF＝36，结论②正确；

③由△ABE和△CBE等高且BE＝3AE，即可得出S△BCE＝3S△ABE，进而可得出S△ABE＝12，结论③正确；

④假设△AEF∽△ACD，根据相似三角形的性质可得出∠AEF＝∠ACD，进而可得出BF∥CD，根据平行四边形的性质可得出AB∥CD，由AB、BF不共线可得出假设不成立，即AEF和△ACD不相似，结论④错误．综上即可得出结论．

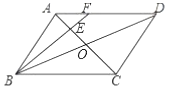
①∵四边形为平行四边形，

∴，，．

∵点是的中点，

∴．

∵，

∴，

∴，

∴，

∴，结论①正确；

②∵，，

∴，

∴，结论②正确；

③∵和等高，且，

∴，

∴，结论③正确；

④假设，则，

∴，即．

∵，

∴和共线．

∵点为的中点，即与不共线，

∴假设不成立，即和不相似，结论④错误．

综上所述：正确的结论有①②③．

故选：D．