题目内容
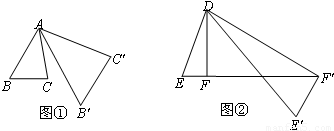
如图，在△DEF中，∠E=90°，∠F=15°，HG是FD的垂直平分线，垂足为H，交FE与G，若DE=5，求FG的长．分析：如图，连接GD．由线段垂直平分线的性质得到FG=DG，则∠F=∠FDG=15°，所以由三角形外角的性质求得∠DGE=30°，在直角三角形中，由“30度角所对的直角边等于斜边的一半”求得所以FG=DG=10．
解答：
解：如图，连接GD．
∵HG是FD的垂直平分线，
∴FG=DG，
∴∠F=∠FDG=15°，
∴∠DGE=∠F+∠FDG=30°，
又∵∠E=90°，
∴GD=2DE=10，
∴FG=10．
解：如图，连接GD．∵HG是FD的垂直平分线，
∴FG=DG，
∴∠F=∠FDG=15°，
∴∠DGE=∠F+∠FDG=30°，
又∵∠E=90°，
∴GD=2DE=10，
∴FG=10．
点评：本题考查了线段垂直平分线的性质和含30度角的直角三角形．垂直平分线上任意一点，到线段两端点的距离相等．
练习册系列答案
相关题目
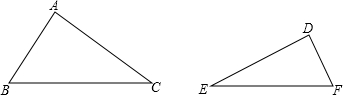
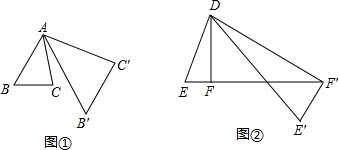
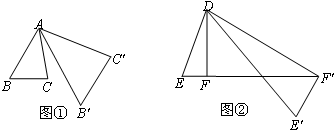
，我们将这种变换记为[θ，n] ．如图②，在△DEF中，∠DFE=90°，将△DEF绕点D旋转，作变换[60°，n]得△DE′F′，如果点E、F、F′恰好在同一直线上，那么n= ．
，我们将这种变换记为[θ，n] ．如图②，在△DEF中，∠DFE=90°，将△DEF绕点D旋转，作变换[60°，n]得△DE′F′，如果点E、F、F′恰好在同一直线上，那么n= ．
