题目内容
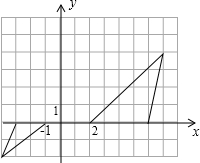 某学习小组在讨论“变化的三角形”时,知道大三角形与小三角形是位似图形(如图所示).则小三角形上的顶点(a,b)对应于大三角形上的顶点( )
某学习小组在讨论“变化的三角形”时,知道大三角形与小三角形是位似图形(如图所示).则小三角形上的顶点(a,b)对应于大三角形上的顶点( )| A、(-2a,-2b) | B、(2a,2b) | C、(-2b,-2a) | D、(-2a,-b) |
分析:过C作CR⊥X轴于R,CK⊥Y轴于K,过F作FG⊥X轴于G,FH⊥Y轴于H,根据中心对称图形的性质和位似图形性质得出
=
=
,根据平行线分线段成比例定理得到
=
=
=
,把(a,b)代入即可求出答案.
| OB |
| OE |
| OA |
| OD |
| 1 |
| 2 |
| OC |
| OF |
| OR |
| OG |
| CK |
| FH |
| 1 |
| 2 |
解答: 解:过C作CR⊥X轴于R,CK⊥Y轴于K,过F作FG⊥X轴于G,FH⊥Y轴
解:过C作CR⊥X轴于R,CK⊥Y轴于K,过F作FG⊥X轴于G,FH⊥Y轴
根据图象得:
=
,
∵大三角形与小三角形是位似图形,
∴
=
=
=
,
根据平行线分线段成比例定理得:
=
=
=
,
∵CR=OK=-b,CK=OR=-a,
∴FH=OG=-2a,FG=-2b,
∴小三角形上的顶点(a,b)对应于大三角形上的顶点是(-2a,-2b),
故选A
 解:过C作CR⊥X轴于R,CK⊥Y轴于K,过F作FG⊥X轴于G,FH⊥Y轴
解:过C作CR⊥X轴于R,CK⊥Y轴于K,过F作FG⊥X轴于G,FH⊥Y轴根据图象得:
| OA |
| OD |
| 1 |
| 2 |
∵大三角形与小三角形是位似图形,
∴
| OB |
| OE |
| OA |
| OD |
| OC |
| OF |
| 1 |
| 2 |
根据平行线分线段成比例定理得:
| OC |
| OF |
| OR |
| OG |
| CK |
| FH |
| 1 |
| 2 |
∵CR=OK=-b,CK=OR=-a,
∴FH=OG=-2a,FG=-2b,
∴小三角形上的顶点(a,b)对应于大三角形上的顶点是(-2a,-2b),
故选A
点评:本题主要考查对位似变换,平行线分线段成比例定理,关于原点对称的点的坐标等知识点的理解和掌握,能熟练地利用性质进行计算是解此题的关键.

练习册系列答案
相关题目
 10、某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形(如图所示).则小鱼上的点(a,b)对应大鱼上的点( )
10、某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形(如图所示).则小鱼上的点(a,b)对应大鱼上的点( ) 18、某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形(如图).则小鱼上的点(a,b)对应大鱼上的点是
18、某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形(如图).则小鱼上的点(a,b)对应大鱼上的点是 11、某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形(如图所示).则小鱼上的点(a,b)对应大鱼上的点( )
11、某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形(如图所示).则小鱼上的点(a,b)对应大鱼上的点( )