题目内容
【题目】已知二次函数
（1）当k=3时，求函数图像与x轴的交点坐标；
（2）函数图像的对称轴与原点的距离为3，求k的值
（3）设二次函数图像上的一点P（x，y）满足
时，y≤2，求k的取值范围。
【答案】（1）（
），（
）；（2）k=4，或k=-2；（3）k≥3
【解析】
（1）把k=3代入解析式，令y=0求出就是与x轴的交点；（2）函数图像的对称轴与原点的距离为3，即对称轴为x=3或x=-3，根据对称轴公式计算即可；（3）函数图像与y轴的交点坐标为（0,2），开口向上，所以对称轴≥2解出即可
（1）当k=3时，令y=0，
解得函数与x轴的两个交点坐标为（），（）
（2）∵函数图像的对称轴与原点的距离为3，
∴
解得，k=4或k=-2
（3）∵函数图像与y轴的交点坐标为（0,2），开口向上，
时，y≤2，
∴函数的对称轴
，k≥3
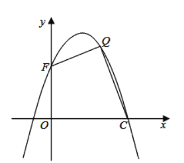
津桥教育计算小状元系列答案
【题目】已知二次函数y＝﹣x2+bx+c，函数值y与自变量x之间的部分对应值如下表：
x | … | ﹣4 | ﹣1 | 0 | 1 | … |
y | … | ﹣2 | ﹣1 | ﹣2 | ﹣7 | … |
（1）此二次函数图象的对称轴是直线，此函数图象与x轴交点个数为 ．
（2）求二次函数的函数表达式；
（3）当﹣5＜x＜﹣1时，请直接写出函数值y的取值范围．
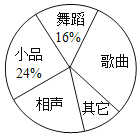
【题目】某校为了庆祝建国七十周年，决定举办一台文艺晚会，为了了解学生最喜爱的节目形式，随机抽取了部分学生进行调查，规定每人从“歌曲”，“舞蹈”，“小品”，“相声”和“其它”五个选项中选择一个，并将调查结果绘制成如下两幅不完整的统计图表，请根据图中信息，解答下列题：
最喜爱的节目 | 人数 |
歌曲 | 15 |
舞蹈 | a |
小品 | 12 |
相声 | 10 |
其它 | b |
（1）在此次调查中，该校一共调查了 名学生；
（2）a＝ ；b＝ ；
（3）在扇形计图中，计算“歌曲”所在扇形的圆心角的度数；
（4）若该校共有1200名学生，请你估计最喜爱“相声”的学生的人数．
【题目】某学校八年级共400名学生，为了解该年级学生的视力情况，从中随机抽取40名学生的视力数据作为样本，数据统计如下：
4.2 4.1 4.7 4.1 4.3 4.3 4.4 4.6 4.1 5.2
5.2 4.5 5.0 4.5 4.3 4.4 4.8 5.3 4.5 5.2
4.4 4.2 4.3 5.3 4.9 5.2 4.9 4.8 4.6 5.1
4.2 4.4 4.5 4.1 4.5 5.1 4.4 5.0 5.2 5.3
根据数据绘制了如下的表格和统计图：
等级 | 视力（x） | 频数 | 频率 |
|
| 4 | 0.1 |
|
| 12 | 0.3 |
|
|
| |
|
|
| |
| 10 | 0.25 | |
合计 | 40 | 1 | |
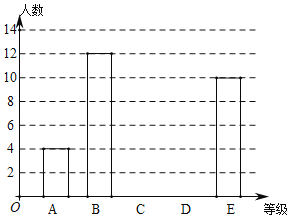
根据上面提供的信息，回答下列问题：
（1）统计表中的
，
；
（2）请补全条形统计图；
（3）根据抽样调查结果，请估计该校八年级学生视力为“
级”的有多少人？
（4）该年级学生会宣传部有2名男生和2名女生，现从中随机挑选2名同学参加“防控近视，爱眼护眼”宣传活动，请用树状图法或列表法求出恰好选中“1男1女”的概率．