题目内容
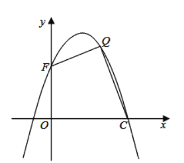
【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() ,
,![]() 两点,且抛物线经过点
两点,且抛物线经过点![]()

(1)求抛物线的解析式.
(2)点![]() 是抛物线上的一个动点(不与点
是抛物线上的一个动点(不与点![]() 点
点![]() 重合),过点
重合),过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .当
.当![]() 时,求
时,求![]() 点坐标;
点坐标;
(3)如图所示,设抛物线与![]() 轴交于点
轴交于点![]() ,在抛物线的第一象限内,是否存在一点
,在抛物线的第一象限内,是否存在一点![]() ,使得四边形
,使得四边形![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 点坐标为(2,9)或(6,-7);(3)存在点Q(
点坐标为(2,9)或(6,-7);(3)存在点Q(![]() )使得四边形OFQC的面积最大,见解析.
)使得四边形OFQC的面积最大,见解析.
【解析】
(1)先由点![]() 在直线
在直线![]() 上求出点
上求出点![]() 的坐标,再利用待定系数法求解可得;
的坐标,再利用待定系数法求解可得;
(2)可设出![]() 点坐标,则可表示出
点坐标,则可表示出![]() 、
、![]() 的坐标,从而可表示出
的坐标,从而可表示出![]() 和
和![]() 的长,由条件可知到关于
的长,由条件可知到关于![]() 点坐标的方程,则可求得
点坐标的方程,则可求得![]() 点坐标;
点坐标;
(3)作![]() 轴于点
轴于点![]() ,设
,设![]() ,
,![]() ,知
,知![]() ,
,![]() ,
,![]() ,根据四边形
,根据四边形![]() 的面积
的面积![]() 建立关于
建立关于![]() 的函数,再利用二次函数的性质求解可得.
的函数,再利用二次函数的性质求解可得.
解:(1)![]() 点
点![]() 在直线
在直线![]() 上,
上,
![]() ,
,![]() ,
,
把![]() 、
、![]() 、
、![]() 三点坐标代入抛物线解析式可得
三点坐标代入抛物线解析式可得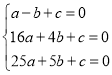 ,解得
,解得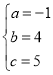 ,
,
![]() 抛物线解析式为
抛物线解析式为![]() ;
;
(2)设![]() ,则
,则![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,解得
时,解得![]() 或
或![]() ,但当
,但当![]() 时,
时,![]() 与
与![]() 重合不合题意,舍去,
重合不合题意,舍去,
![]() ;
;
当![]() 时,解得
时,解得![]() 或
或![]() ,但当
,但当![]() 时,
时,![]() 与
与![]() 重合不合题意,舍去,
重合不合题意,舍去,
![]() ;
;
综上可知![]() 点坐标为
点坐标为![]() 或
或![]() ;
;
(3)存在这样的点![]() ,使得四边形
,使得四边形![]() 的面积最大.
的面积最大.
如图,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
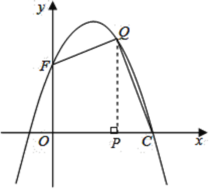
设![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
四边形![]() 的面积
的面积![]()
![]()
![]()
![]() ,
,
当![]() 时,四边形
时,四边形![]() 的面积取得最大值,最大值为
的面积取得最大值,最大值为![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]() ,
,![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】我市一水果销售公司,需将一批鲜桃运往某地,有汽车、火车、运输工具可供选择,两种运输工具的主要参考数据如下:
运输工具 | 途中平均速度(单位:千米/时) | 途中平均费用(单位:元/千米) | 装卸时间(单位:小时) | 装卸费用(单位:元) |
汽车 | 75 | 8 | 2 | 1000 |
火车 | 100 | 6 | 4 | 2000 |
若这批水果在运输过程中(含装卸时间)的损耗为150元/时,设运输路程为x(![]() )千米,用汽车运输所需总费用为y1元,用火车运输所需总费用为y2元.
)千米,用汽车运输所需总费用为y1元,用火车运输所需总费用为y2元.
(1)分别求出y1、y2与x的关系式;
(2)那么你认为采用哪种运输工具比较好?


