Question

【题目】已知关于x的一元二次方程.

（1）证明该方程一定有两个不相等的实数根；

（2）设该方程两根为x1、x2（x1<x2）.

①当时，试确定y值的范围；

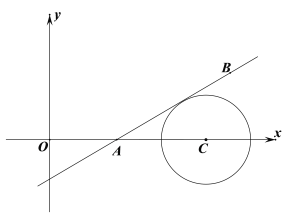
②如图，平面直角坐标系中有三点A、B、C，坐标分别为（x1,0）、（x2,3）、（7，0）.以点C为圆心，2个单位长度为半径的圆与直线AB相切，求n的值.

Answer 1

【答案】（1）见解析；（2）①当n<-3时，y<-3；②n= -

【解析】

（1）根据根的判别式即可证明；

（2）①解方程得，方程两根为3和3-，由n<-3得到<0，故3-，根据y=x2(n+x1) =3n+6，根据一次函数的性质即可求解；

②作CD⊥AB于D，DH⊥AC于H.由①知,A（3,0），由C（7,0），得CA=4，由圆C与直线AB相切，得CD=2,可得AD=2.利用S△ADC=，求得DH=，再得到点D坐标为（6，），求出直线AB的函数关系式为y=，将点B的坐标代入直线方程得n= -，故可求解.

（1）因为△=9>0,

所以该方程一定有两个不相等的实数根；

（2）①

故方程两根为3和3-，

因为n<-3,所以n+3<0,

所以<0,

所以3-.

所以x1=3，x2=3-.

故y=x2(n+x1)==3n+6，

y是n的一次函数，

因为3>0，所以y随n的增大而增大，

所以当n<-3时，y<-3.

②作CD⊥AB于D，DH⊥AC于H.

由①知,A（3,0），因为C（7,0），

所以CA=4，

因为圆C与直线AB相切，

所以CD=2,

可得AD==2.

因为S△ADC=，

即2，所以DH=，∴AH==3

∴点D坐标为（6，）.

设直线AB的函数关系式为y=kx+b，代入A（3,0）、D（6，）

得，解得，.

所以直线AB的函数关系式为y=.

将点B的坐标代入直线方程得，×=3,

解得，n= -，经检验， n= -是方程的解，

所以n= -