题目内容
已知?ABCD的对角线AC、BD相交于点O,AC=16cm,BD=12cm,BC=10cm,则△OAD的周长是分析:求三角形的周长,找到各边长即可.利用平行四边形的性质,对角线互相平分对边相等可以求解.
解答: 解:如图:∵ABCD为平行四边形,
解:如图:∵ABCD为平行四边形,
∴对角线互相平分,对边相等,
即OA=OC=8、OB=OD=6,AD=BC=10,
∴△OAD的周长为OA+OD+AD=8+6+10=24cm.
∵OD=6,OA=8,AD=10,
可知BD⊥AC,
∴?ABCD的面积=
AC×BD=96cm2.
故答案为:24cm;96cm2.
 解:如图:∵ABCD为平行四边形,
解:如图:∵ABCD为平行四边形,∴对角线互相平分,对边相等,
即OA=OC=8、OB=OD=6,AD=BC=10,
∴△OAD的周长为OA+OD+AD=8+6+10=24cm.
∵OD=6,OA=8,AD=10,
可知BD⊥AC,
∴?ABCD的面积=
| 1 |
| 2 |
故答案为:24cm;96cm2.
点评:本题考查了平行四边形的性质.属于单一考点的问题,必须熟练地掌握.

练习册系列答案
相关题目
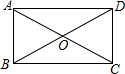 已知?ABCD的对角∠BAD和∠BCD互补.
已知?ABCD的对角∠BAD和∠BCD互补.
 如图,EF过平行四边形ABCD的对角形的交点O,交AD于点E,交BC于点F,已知AB=5,BC=6,OE=2,那么四边形EFCD的周长是
如图,EF过平行四边形ABCD的对角形的交点O,交AD于点E,交BC于点F,已知AB=5,BC=6,OE=2,那么四边形EFCD的周长是 已知?ABCD的对角∠BAD和∠BCD互补.
已知?ABCD的对角∠BAD和∠BCD互补. +1,BD=3+
+1,BD=3+ ,
,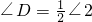 .∵∠1+∠2=360°∴
.∵∠1+∠2=360°∴ ,同理∠BAD+∠BCD=180°,即圆内接四边形对角(相对的两个角)互补.
,同理∠BAD+∠BCD=180°,即圆内接四边形对角(相对的两个角)互补.