题目内容
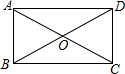已知?ABCD的对角∠BAD和∠BCD互补．（1）求∠BAD的度数；
（2）若AC=x+
| 3 |
| 3 |
分析：（1）根据平行四边形的性质，知∠BAD和∠BCD，又因为∠BAD和∠BCD互补，即可求出∠BAD的度数；
（2）有意可判断出?ABCD为矩形，得知其对角线相等，列出方程即可解答．
（2）有意可判断出?ABCD为矩形，得知其对角线相等，列出方程即可解答．
解答：解：（1）∵?ABCD的对角∠BAD和∠BCD互补，
又∵∠BAD=∠BCD，
∴∠BCD=90°；
（2）由（1）可知，?ABCD为矩形，
∴AC=BD，
∴x+
+1=3+
-x，
∴x=1．
故答案为：90°，1．
又∵∠BAD=∠BCD，
∴∠BCD=90°；
（2）由（1）可知，?ABCD为矩形，
∴AC=BD，
∴x+
| 3 |
| 3 |
∴x=1．
故答案为：90°，1．
点评：此题不仅考查了矩形的判定，还考查了矩形的性质，要先说它是矩形，再说它对角相等、对角线相等且互相平分．
练习册系列答案
相关题目
如图，EF过平行四边形ABCD的对角形的交点O，交AD于点E，交BC于点F，已知AB=5，BC=6，OE=2，那么四边形EFCD的周长是
已知?ABCD的对角∠BAD和∠BCD互补．
+1，BD=3+
，
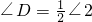．∵∠1+∠2=360°∴
，同理∠BAD+∠BCD=180°，即圆内接四边形对角（相对的两个角）互补．