题目内容

若a、b、c是非零实数，且满足 $数学公式$ ，直线y=kx+b经过点（4，0），求直线y=kx+b与两坐标轴所围成的三角形的面积．

解：∵ $\text{[math]}$
∴a=（b+c）k，b=（a+c）k，c=（a+b）k，
∴a+b+c=2（a+b+c）k，
∴①当a+b+c≠0时，k= $\text{[math]}$ ，
∴y=kx+b变为：y= $\text{[math]}$ x+b，
∵经过点（4，0），
∴ $\text{[math]}$ ×4+b=0，
b=-2，
∴y= $\text{[math]}$ x-2，
图象如右图：S_△ABO= $\text{[math]}$ ×AO×BO= $\text{[math]}$ ×2×4=4．
②当a+b+c=0时，a=-（b+c），
k= 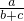$\text{[math]}$ =-1
同法可请求：y=-x+4，
S_△ADO=8，
即直线y=kx+b与两坐标轴所围成的三角形的面积是4或8．
分析：首先根据条件 $\text{[math]}$ ，根据a+b+c=0和a+b+c≠0，可得到直线y=kx+b中的k值，再根据经过点（4，0）可求出b的值，从而得到函数关系式，然后画出函数图象即可求出与两坐标轴所围成的三角形的面积，
点评：此题主要考查了待定系数法求一次函数解析式以及画函数图象，画一次函数y=kx+b的图象经过（0，b）（- $\text{[math]}$ ，0），画出图象后再求与两坐标轴所围成的三角形的面积比较直观，分类讨论思想的运用．