题目内容
 如图,Rt△ABC中,∠ACB=90°,点O、I分别为△ABC的外心和内心,AC=6,BC=8,则OI的值为
如图,Rt△ABC中,∠ACB=90°,点O、I分别为△ABC的外心和内心,AC=6,BC=8,则OI的值为
- A.2
- B.

- C.

- D.1
C
分析:如图,作△ABC的内切圆⊙I,过点I作ID⊥BC于D,IE⊥AC于E,IN⊥AB于N.先根据勾股定理求出AB=10,得到△ABC的外接圆半径AO=5,再证明四边形IECD是正方形,根据内心的性质和切线长定理
求出⊙I的半径r=2,则ON=1,然后在Rt△OIN中,运用勾股定理即可求解.
解答: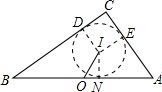 解:如图,作△ABC的内切圆⊙I,过点I作ID⊥BC于D,IE⊥AC于E,IN⊥AB于N.
解:如图,作△ABC的内切圆⊙I,过点I作ID⊥BC于D,IE⊥AC于E,IN⊥AB于N.
在Rt△ABC中,∵∠ACB=90°,AC=6,BC=8,
∴AB= =10.
=10.
∵点O为△ABC的外心,
∴AO为外接圆半径,AO= AB=5.
AB=5.
设⊙I的半径为r,则ID=IE=r,
又∵∠IDC=∠IEC=∠C=90°,
∴四边形IECD是正方形,
∴CE=CD=r,AE=AN=6-r,BD=BN=8-r,
∵AB=10,
∴8-r+6-r=10,
解得r=2,
∴IN=r=2,AN=6-r=4.
在Rt△OIN中,∵∠INO=90°,ON=AO-AN=5-4=1,
∴OI=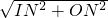 =
= .
.
故选C.
点评:此题考查了直角三角形的外心与内心的概念及性质,勾股定理,正方形的判定与性质,切线长定理,综合性较强,难度适中.求出△ABC的内切圆半径是解题的关键.
分析:如图,作△ABC的内切圆⊙I,过点I作ID⊥BC于D,IE⊥AC于E,IN⊥AB于N.先根据勾股定理求出AB=10,得到△ABC的外接圆半径AO=5,再证明四边形IECD是正方形,根据内心的性质和切线长定理
求出⊙I的半径r=2,则ON=1,然后在Rt△OIN中,运用勾股定理即可求解.
解答:
 解:如图,作△ABC的内切圆⊙I,过点I作ID⊥BC于D,IE⊥AC于E,IN⊥AB于N.
解:如图,作△ABC的内切圆⊙I,过点I作ID⊥BC于D,IE⊥AC于E,IN⊥AB于N.在Rt△ABC中,∵∠ACB=90°,AC=6,BC=8,
∴AB=
 =10.
=10.∵点O为△ABC的外心,
∴AO为外接圆半径,AO=
 AB=5.
AB=5.设⊙I的半径为r,则ID=IE=r,
又∵∠IDC=∠IEC=∠C=90°,
∴四边形IECD是正方形,
∴CE=CD=r,AE=AN=6-r,BD=BN=8-r,
∵AB=10,
∴8-r+6-r=10,
解得r=2,
∴IN=r=2,AN=6-r=4.
在Rt△OIN中,∵∠INO=90°,ON=AO-AN=5-4=1,
∴OI=
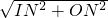 =
= .
.故选C.
点评:此题考查了直角三角形的外心与内心的概念及性质,勾股定理,正方形的判定与性质,切线长定理,综合性较强,难度适中.求出△ABC的内切圆半径是解题的关键.

练习册系列答案
相关题目

 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB= 如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( )
如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( ) 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F. 如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.
如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.