题目内容
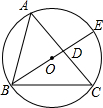如图，△ABC的外接圆⊙O的直径BE交AC于点D，已知弧BC等于120°，cotC=| 2 |
| 3 |
| 3 |
| 3 |
| A、没有实数恨 |
| B、有两个相等的正实数根 |
| C、有两个相等的实数根 |
| D、有两个不相等的正实数根 |
分析：BD为直径，连接CE，构成直角三角形．
过D点作DF⊥BC．在Rt△CDF中，运用锐角三角函数求边长；
在Rt△BCE中，因为弧BC等于120°，可求其两锐角分别为60°、30°，根据锐角三角函数可求BD、DE的长，代入判别式中，确定判别式的符号．
过D点作DF⊥BC．在Rt△CDF中，运用锐角三角函数求边长；
在Rt△BCE中，因为弧BC等于120°，可求其两锐角分别为60°、30°，根据锐角三角函数可求BD、DE的长，代入判别式中，确定判别式的符号．
解答：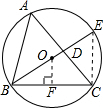
解：过D点作DF⊥BC，垂足为点F，连接CE．
在Rt△CDF中，cotC=
．
设CF=2，则DF=
．
已知弧BC等于120°，BE为直径，
所以∠E=60°，∠ECB=90°，∠EBC=30°．
在Rt△BDF中，BD=2DF=2
，BF=3．
在Rt△BCE中，BC=BF+CF=5，BE=
=
，
DE=BE-BD=
．
∵△=（
BD）2-4•BD•DE
=（
×2
）2-4×2
×
=36-32=4＞0，
又x1+x2=
BD＞0，x1•x2=BD•DE＞0，
∴方程有两个不相等的正实数根，故选D．
解：过D点作DF⊥BC，垂足为点F，连接CE．在Rt△CDF中，cotC=
| 2 |
| 3 |
| 3 |
设CF=2，则DF=
| 3 |
已知弧BC等于120°，BE为直径，
所以∠E=60°，∠ECB=90°，∠EBC=30°．
在Rt△BDF中，BD=2DF=2
| 3 |
在Rt△BCE中，BC=BF+CF=5，BE=
| 5 |
| cos30° |
10
| ||
| 3 |
DE=BE-BD=
4
| ||
| 3 |
∵△=（
| 3 |
=（
| 3 |
| 3 |
| 3 |
4
| ||
| 3 |
=36-32=4＞0，
又x1+x2=
| 3 |
∴方程有两个不相等的正实数根，故选D．
点评：本题是圆的问题、锐角三角函数与一元二次方程根的判别式的综合运用，一般需要把问题转化到直角三角形中，利用锐角三角函数设边长，求边长，再用判别式判断方程根的情况．
练习册系列答案
相关题目
如图，半圆O为△ABC的外接半圆，AC为直径，D为劣弧
（2013•沙湾区模拟）如图，△ABC的外接⊙O的半径为R，高为AD，∠BAC的平分线交⊙O、BC于E、P，EF切⊙O交AC的延长线于F．
如图，⊙O是△ABC的
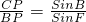如图，△ABC的外接⊙O的半径为R，高为AD，∠BAC的平分线交⊙O、BC于E、P，EF切⊙O交AC的延长线于F．
．
如图，△ABC的外接⊙O的半径为R，高为AD，∠BAC的平分线交⊙O、BC于E、P，EF切⊙O交AC的延长线于F．
．