题目内容
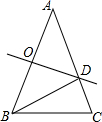 如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD.则下列结论:①∠C=2∠A;②BD平分∠ABC;③BC=AD;④CD=OD.正确的有( )
如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD.则下列结论:①∠C=2∠A;②BD平分∠ABC;③BC=AD;④CD=OD.正确的有( )| A、1个 | B、2个 | C、3个 | D、4个 |
考点:线段垂直平分线的性质,等腰三角形的判定与性质
专题:
分析:由在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,根据线段垂直平分线的性质与等腰三角形的性质,可求得∠ABD=∠DBC=∠A=36°,∠ABC=∠BDC=∠C=72°,继而求得:①∠C=2∠A;②BD平分∠ABC;③BC=AD.
解答:解:∵AB的垂直平分线OD交AB于点O,交AC于点D,
∴AD=BD,
∴∠ABD=∠A=36°,
∵AB=AC,
∴∠ABC=∠C=72°,
∴∠C=2∠A,故①正确;
∴∠DBC=∠ABC-∠ABD=36°,
∴∠ABD=∠DBC,
∴BD平分∠ABC,故②正确;
∴∠BDC=∠C=72°,
∴BC=BD=AD,故③正确;
∵DO⊥AB,DC不垂直BC,BD平分∠ABC,
∴CD≠OD,故④错误.
故选C.
∴AD=BD,
∴∠ABD=∠A=36°,
∵AB=AC,
∴∠ABC=∠C=72°,
∴∠C=2∠A,故①正确;
∴∠DBC=∠ABC-∠ABD=36°,
∴∠ABD=∠DBC,
∴BD平分∠ABC,故②正确;
∴∠BDC=∠C=72°,
∴BC=BD=AD,故③正确;
∵DO⊥AB,DC不垂直BC,BD平分∠ABC,
∴CD≠OD,故④错误.
故选C.
点评:此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 如图,在?ABCD中,AB=3cm,AD=5cm,BD的垂直平分线分别交AD、BC于F、E,则△CDE的周长为( )
如图,在?ABCD中,AB=3cm,AD=5cm,BD的垂直平分线分别交AD、BC于F、E,则△CDE的周长为( )| A、8cm | B、11cm |
| C、13cm | D、14cm |
新定义运算a*b=a(a-b),则3*4的结果是( )
| A、12 | B、4 | C、3 | D、-3 |
已知样本数据1、2、4、3、5,下列说法不正确的是( )
| A、极差是4 | B、平均数是3 |
| C、中位数是4 | D、方差是2 |
下列线段的长度能围成三角形的是( )
| A、1cm,2cm,3cm |
| B、2cm,5cm,3cm |
| C、3cm,4cm,5cm |
| D、4cm,4cm,9cm. |
 ?根据2014年11月份的月历表,思考并回答如下问题:
?根据2014年11月份的月历表,思考并回答如下问题: