Question

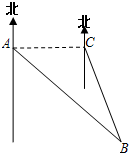（2013•徐汇区一模）如图，小岛B正好在深水港口A的东南方向，一艘集装箱货船从港口A出发，沿正东方向以每小时30千米的速度行驶，40分钟后在C处测得小岛B在它的南偏东15°方向，求小岛B离开深水港口A的距离．（精确到0.1千米）
参考数据：

2

≈1.41，

6

≈2.45，sin15°≈0.26，cos15°≈0.97，tan15°≈0.27．

Answer 1

分析：过点C作CD⊥AB，垂足为D，则在Rt△ADC和Rt△BDC中，利用三角函数即可用PD表示出AD与BD，根据AB=AD+BD即可求得AB的长．

解答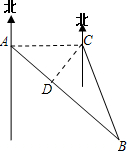：解：由题意，得AC=30×

2

3

=20．  …（2分）
[方法一]过点C作CD⊥AB，垂足为D．…（1分）
在Rt△ADC中，∠ADC=90°，∠CAD=45°
∴AD=ACcos45°=10

2

，CD=ACsin45°=10

2

…（2分）
在Rt△BDC中，∠BDC=90°，∠B=90°-45°-15°=30°…（1分）
∴BD=CDcot30°=10

6

…（2分）
∴AB=AD+BD=10(

2

+

6

)≈10×（1.41+2.45）=38.6．…（2分）
[方法二]过点B作BD⊥AC，交AC延长线于D． …（1分）
在Rt△BDC中，∠BDC=90°，∠CBD=15°
设BD=x，则CD=BDtan15°≈0.27x．  …（2分）
∵∠ABD=90°-∠DAB=90°-45°=45°=∠DAB…（1分）
∴AD=BD，
∴20+0.27x=x，得x=

20

0.73

…（2分）
∴AB=

2

BD=

2

×

20

0.73

≈1.41×

20

0.73

≈38.6．
答：小岛B离开深水港口A的距离是38.6千米．

点评：考查了解直角三角形的应用-方向角问题，解一般三角形，求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．