题目内容
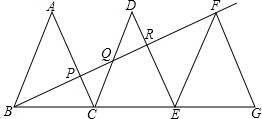
已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=| 3 |
(1)求证:△BFG∽△FEG;
(2)求出BF的长;
(3)求
| BP |
| QR |
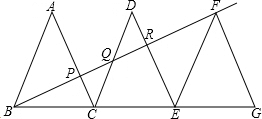
分析:(1)由题意得出FG=
,GE=1,BG=3,则
=
,再由∠FGE=∠BGF,得△BFG∽△FEG;
(2)根据△BFG∽△FEG,得
=
,再由FG=FE,求出BF即可;
(3)根据相似三角形的性质直接得出答案即可.
| 3 |
| FG |
| BG |
| EG |
| FG |
(2)根据△BFG∽△FEG,得
| FG |
| BG |
| FE |
| BF |
(3)根据相似三角形的性质直接得出答案即可.
解答:解:(1)证明:∵△ABC、△DCE、△FEG是三个全等的等腰三角形,
∴FG=AB=
,GE=BC=1,BG=3BC=3,
∴
=
,
=
=
,
∴
=
,
∵∠FGE=∠BGF,
∴△BFG∽△FEG;
(2)由(1)知:△BFG∽△FEG,
∴
=
,
∵FG=FE,
∴BF=BG=3;
(3)∵△ABC、△DCE、△FEG是三个全等的等腰三角形,
∴∠ACB=∠DEC,BC=CE,
∴AC∥DE,
∴
=
,
∴BP=PR,
同理:CQ∥EF,
∴CQ=
EF,
∴CQ=DQ,
∵AC∥DE,
∴△PCQ∽△RDQ,
∴PQ=QR,
∴BP=2QR,
∴
=2.
∴FG=AB=
| 3 |
∴
| FG |
| BG |
| ||
| 3 |
| EG |
| FG |
| 1 | ||
|
| ||
| 3 |
∴
| FG |
| BG |
| EG |
| FG |
∵∠FGE=∠BGF,
∴△BFG∽△FEG;
(2)由(1)知:△BFG∽△FEG,
∴
| FG |
| BG |
| FE |
| BF |

∵FG=FE,
∴BF=BG=3;
(3)∵△ABC、△DCE、△FEG是三个全等的等腰三角形,
∴∠ACB=∠DEC,BC=CE,
∴AC∥DE,
∴
| BP |
| PR |
| BC |
| CE |
∴BP=PR,
同理:CQ∥EF,
∴CQ=
| 1 |
| 2 |
∴CQ=DQ,
∵AC∥DE,
∴△PCQ∽△RDQ,
∴PQ=QR,
∴BP=2QR,
∴
| BP |
| QR |
点评:本题考查了相似三角形的判定和性质以及等腰三角形的性质,是基础知识要熟练掌握.

练习册系列答案
相关题目
 如图,已知△ABC中,∠C=90°,∠BAC=2∠B,D是BC上一点,DE⊥AB于E,DE=DC.求证:AD=BD.
如图,已知△ABC中,∠C=90°,∠BAC=2∠B,D是BC上一点,DE⊥AB于E,DE=DC.求证:AD=BD.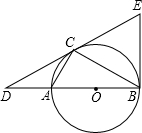 (1)求∠CDB的度数;
(1)求∠CDB的度数; 如图,已知△ABC中,AE:EB=1:3,BD:DC=2:1,AD与CE相交于F.求
如图,已知△ABC中,AE:EB=1:3,BD:DC=2:1,AD与CE相交于F.求