��Ŀ����
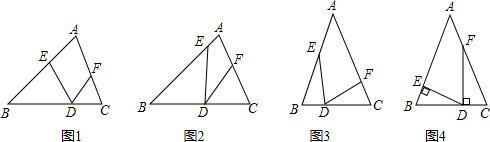
��֪��ABC�У���A=������D��E��F�ֱ���BC��AB��AC�ϣ�
��1����ͼ1����BE=BD��CD=CF�����EDF=
��2����ͼ2����BD=DE��DC=DF�����EDF=
��3����ͼ3����BD=CF��CD=BE��AB=AC�����EDF=
��2����ͼ4����DE��AB��DF��BC��AB=AC�����EDF=
��1����ͼ1����BE=BD��CD=CF�����EDF=
90��-
��
| 1 |
| 2 |
90��-
��
��| 1 |
| 2 |
��2����ͼ2����BD=DE��DC=DF�����EDF=
180��-2��
180��-2��
����3����ͼ3����BD=CF��CD=BE��AB=AC�����EDF=
90��-
��
| 1 |
| 2 |
90��-
��
��| 1 |
| 2 |
��2����ͼ4����DE��AB��DF��BC��AB=AC�����EDF=
90��-
��
| 1 |
| 2 |
90��-
��
��| 1 |
| 2 |

��������1���ɡ�ABC�У���A=��������á�B+��C��ֵ������BE=BD��CD=CF�����ݵ��������ε����ʣ�������á�BDE+��CDF��ֵ���̶���ô𰸣�
��2���ɡ�ABC�У���A=��������á�B+��C��ֵ������BD=DE��DC=DF�����ݵ��������ε����ʣ�������á�BDE+��CDF��ֵ���̶���ô𰸣�
��3���ɡ�ABC�У���A=����AB=AC������á�B��ֵ����֤�á�BDE�ա�CFD���̶�����á�EDF=��B��
��4���ɡ�ABC�У���A=����AB=AC������á�B��ֵ������DE��AB��DF��BC������á�EDF=��B��
��2���ɡ�ABC�У���A=��������á�B+��C��ֵ������BD=DE��DC=DF�����ݵ��������ε����ʣ�������á�BDE+��CDF��ֵ���̶���ô𰸣�
��3���ɡ�ABC�У���A=����AB=AC������á�B��ֵ����֤�á�BDE�ա�CFD���̶�����á�EDF=��B��
��4���ɡ�ABC�У���A=����AB=AC������á�B��ֵ������DE��AB��DF��BC������á�EDF=��B��
����⣺��1���ߡ�A=����
���B+��C=180��-����
��BE=BD��CD=CF��
���BED=��BDE����CFD=��CDF��
���BDE+��CDF=
��180��-��B��+
��180��-��C��=180��-
����B+��C��=90��+
����
���EDF=180��-����BDE+��CDF��=90��-
����
��2���ߡ�A=����
���B+��C=180��-����
��BD=DE��DC=DF��
���BED=��B����CFD=��C��
���BDE=180��-2��B����CDF=180��-2��C��
���BDE=180��-����BED+��CDF��=2����B+��C��-180��=180��-2����
��3����AB=AC����A=����
���B=��C=90��-
����
�ڡ�BDE�͡�CFD�У�
��
���BDE�ա�CFD��SAS����
���BED=��CDF��
�ߡ�B+��BDE+��BED=180�㣬��BDE+��CDF+��EDF=180�㣬
���EDF=��B=90��-
����
��4����AB=AC����A=����
���B=��C=90��-
����
��DE��AB��DF��BC��
���BDE+��EDF=90�㣬��B+��BDE=90�㣬
���EDF=��B=90��-
����
�ʴ�Ϊ����1��90��-
������2��180��-2������3��90��-
������4��90��-
����
���B+��C=180��-����
��BE=BD��CD=CF��
���BED=��BDE����CFD=��CDF��
���BDE+��CDF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
���EDF=180��-����BDE+��CDF��=90��-
| 1 |
| 2 |
��2���ߡ�A=����
���B+��C=180��-����
��BD=DE��DC=DF��
���BED=��B����CFD=��C��
���BDE=180��-2��B����CDF=180��-2��C��
���BDE=180��-����BED+��CDF��=2����B+��C��-180��=180��-2����
��3����AB=AC����A=����
���B=��C=90��-
| 1 |
| 2 |
�ڡ�BDE�͡�CFD�У�
|
���BDE�ա�CFD��SAS����
���BED=��CDF��
�ߡ�B+��BDE+��BED=180�㣬��BDE+��CDF+��EDF=180�㣬
���EDF=��B=90��-
| 1 |
| 2 |
��4����AB=AC����A=����
���B=��C=90��-
| 1 |
| 2 |
��DE��AB��DF��BC��
���BDE+��EDF=90�㣬��B+��BDE=90�㣬
���EDF=��B=90��-
| 1 |
| 2 |
�ʴ�Ϊ����1��90��-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
���������⿼���˵��������ε����ʡ�ȫ�������ε��ж��������Լ��������ڽǺͶ����������Ѷ����У�ע�����շ���˼�������ν��˼���Ӧ�ã�

��ϰ��ϵ�д�
�����Ŀ
 ������������ܣ���˵�����ɣ�
������������ܣ���˵�����ɣ� ��֪��ABC�У�DE��BC��EF��AB��AB=3��BC=6��AD��DB=2��1�����ı���DBFE���ܳ�Ϊ
��֪��ABC�У�DE��BC��EF��AB��AB=3��BC=6��AD��DB=2��1�����ı���DBFE���ܳ�Ϊ ��ͼ��ʾ����֪��ABC�У�AB=AC����ABΪֱ������O��BC��D����AC��E����D��DF��AC��F
��ͼ��ʾ����֪��ABC�У�AB=AC����ABΪֱ������O��BC��D����AC��E����D��DF��AC��F ��ͼ����֪��ABC�У�AB=AC��AB��ֱƽ���߽�AC��D������BE������A=40�㣬���EBC=��������
��ͼ����֪��ABC�У�AB=AC��AB��ֱƽ���߽�AC��D������BE������A=40�㣬���EBC=��������