题目内容
 如图,△ABC内接于⊙O,AB是⊙O的直径,延长AB到D,连接CD.请你结合图形,编写一道题.要求:再补充两个已知条件,并写出在所有已知条件下得出的一个结论.例如:
如图,△ABC内接于⊙O,AB是⊙O的直径,延长AB到D,连接CD.请你结合图形,编写一道题.要求:再补充两个已知条件,并写出在所有已知条件下得出的一个结论.例如:“补充已知:OB=BD,CD切⊙O于点C,求证:∠A=∠D”
“补充已知:
求证:
分析:添加∠A=∠D,CD是⊙O的切线,可以通过作辅助线OC,求出∠COB=90°,从而证出
的度数为60°.
 |
| BC |
解答: 解:已知:∠A=∠D,CD是⊙O的切线,
解:已知:∠A=∠D,CD是⊙O的切线,
求证:
的度数为60°.
证明:连接OC,
则∠OCD=90°,
设∠A=∠ACO=∠D=x度,
在△ACO中,∠COD=2x度,
∴在直角三角形OCD中,2x+x=90,
解得x=30,
∴∠COD=60°.
 解:已知:∠A=∠D,CD是⊙O的切线,
解:已知:∠A=∠D,CD是⊙O的切线,求证:
 |
| BC |
证明:连接OC,
则∠OCD=90°,
设∠A=∠ACO=∠D=x度,
在△ACO中,∠COD=2x度,
∴在直角三角形OCD中,2x+x=90,
解得x=30,
∴∠COD=60°.
点评:本题是一道开放题,条件、结论、过程全开放,要有一定的知识积累方可正确解答.

练习册系列答案
相关题目
 15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD=
15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD= 21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.
21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.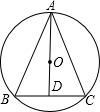 已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积.
已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积. 18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( )
18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( ) 如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.
如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.