题目内容
如图,直线y=﹣x+3与x轴,y轴分别交于B,C两点,抛物线y=﹣x2+bx+c经过B,C两点,点A是抛物线与x轴的另一个交点.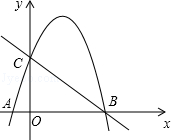
(1)求B、C两点坐标;
(2)求此抛物线的函数解析式;
(3)在抛物线上是否存在点P,使S△PAB=S△CAB,若存在,求出P点坐标,若不存在,请说明理由.
(1)B(3,0)C(0,3)(2)此抛物线的解析式为y=﹣x2+2x+3.(3)存在这样的P点,其坐标为P(0,3),(2,3)(1+ ,﹣3)或(1﹣
,﹣3)或(1﹣ ,﹣3).
,﹣3).
解析试题分析:(1)已知了过B、C两点的直线的解析式,当x=0时可求出C点的坐标,当y=0是可求出B点的坐标.
(2)由于抛物线的解析式中只有两个待定系数,因此将B、C两点的坐标代入抛物线中即可求出抛物线的解析式.
(3)根据(2)的抛物线的解析式可得出A点的坐标,由此可求出AB的长,由于S△PAB=S△CAB,而AB边为定值.由此可求出P点的纵坐标,然后将P点的纵坐标代入抛物线的解析式中即可求出P点的坐标.
试题解析:(1)∵直线y=﹣x+3经过B、C
∴当x=0时y=3
当y=0时x=3
∴B(3,0)C(0,3)
(2)∵抛物线y=﹣x2+bx+c经过B、C
∴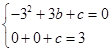 .
.
∴b=2,c=3.
∴此抛物线的解析式为y=﹣x2+2x+3.
(3)当y=0时,﹣x2+2x+3=0;x1=﹣1,x2=3.
∴A(﹣1,0)
设P(x,y)
∵S△PAB=S△CAB
∴ ×4×|y|=
×4×|y|= ×4×3
×4×3
∴y=3或y=﹣3
①当y=3时,3=﹣x2+2x+3
∴x1=0,x2=2
P(0,3)或(2,3)
②当y=﹣3时,﹣3=﹣x2+2x+3
∴x1=1+ ,x2=1﹣
,x2=1﹣
∴P(1+ ,﹣3)或(1﹣
,﹣3)或(1﹣ ,﹣3).
,﹣3).
因此存在这样的P点,其坐标为P(0,3),(2,3)(1+ ,﹣3)或(1﹣
,﹣3)或(1﹣ ,﹣3).
,﹣3).
考点:二次函数综合题.

 阅读快车系列答案
阅读快车系列答案下列方程为一元一次方程的是( )
| A.y+4 = 0 | B.x+2y=3 | C.x2=2x | D. |
一根80厘米的弹簧,一端固定,如果另一端挂上物体,那么在正常情况下物体的质量每增加1千克可使弹簧增长2厘米。(10 分)
(1)填写下表
| 所挂物体的质量(千克) | 1 | 2 | 3 | 4 | … |
| 弹簧的总长度(厘米) | | | | | … |
(2)写出弹簧总长度y(厘米)与所挂物体的质量x(千克)之间的数量关系。
(3)若在这根弹簧上挂上某一物体后,弹簧总长为96 厘米,求所挂物体的质量?
“小刚同学数学考试得满分”是一个( )
| A.必然事件 | B.不可能事件 | C.随机事件 | D.上述说法都不对 |
 =6,3x-y+2z=0,2x+4y,5x-y>0中是二元一次方程的有( )个。
=6,3x-y+2z=0,2x+4y,5x-y>0中是二元一次方程的有( )个。 的图象有两个交点,其中一个交点的横坐标为1,则两个函数图象的交点坐标是 .
的图象有两个交点,其中一个交点的横坐标为1,则两个函数图象的交点坐标是 . 的图象经过点(-l,5),这个函数的表达式为 .
的图象经过点(-l,5),这个函数的表达式为 .
