题目内容
 如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则sin∠B′的值为
如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则sin∠B′的值为
- A.

- B.

- C.

- D.3
B
分析:如图在Rt△BCD中,由CD=1,BD=3,根据勾股定理可计算出BC= ,再根据正弦的定义得到sinB=
,再根据正弦的定义得到sinB= =
= =
= ,然后根据旋转的性质得∠B′=∠B,则有sinB′=sinB=
,然后根据旋转的性质得∠B′=∠B,则有sinB′=sinB= .
.
解答:如图, 设正方形网格中每个小正方形的边长为1,
设正方形网格中每个小正方形的边长为1,
在Rt△BCD中,∵CD=1,BD=3,
∴BC=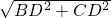 =
=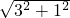 =
= ,
,
∴sinB= =
= =
= ,
,
∵△ABC绕着点A逆时针旋转得到△AC′B′,
∴∠B′=∠B,
∴sinB′= .
.
故选B.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了勾股定理以及三角形函数的定义.
分析:如图在Rt△BCD中,由CD=1,BD=3,根据勾股定理可计算出BC=
 ,再根据正弦的定义得到sinB=
,再根据正弦的定义得到sinB= =
= =
= ,然后根据旋转的性质得∠B′=∠B,则有sinB′=sinB=
,然后根据旋转的性质得∠B′=∠B,则有sinB′=sinB= .
.解答:如图,
 设正方形网格中每个小正方形的边长为1,
设正方形网格中每个小正方形的边长为1,在Rt△BCD中,∵CD=1,BD=3,
∴BC=
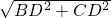 =
=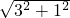 =
= ,
,∴sinB=
 =
= =
= ,
,∵△ABC绕着点A逆时针旋转得到△AC′B′,
∴∠B′=∠B,
∴sinB′=
 .
.故选B.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了勾股定理以及三角形函数的定义.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 9、如图,A、C、E三点在同一条直线上,△DAC和△EBC都是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN.其中,正确结论的个数是( )
9、如图,A、C、E三点在同一条直线上,△DAC和△EBC都是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN.其中,正确结论的个数是( ) 15、如图,A、Q、R三点在一条直线上,S为直线外一点,∠AQS=136°,∠QRS=64°,则∠QSR=( )
15、如图,A、Q、R三点在一条直线上,S为直线外一点,∠AQS=136°,∠QRS=64°,则∠QSR=( )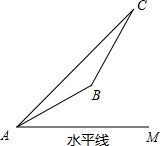 车站B的仰角为30°,AB间缆绳长500米(自然弯曲忽略不计).(
车站B的仰角为30°,AB间缆绳长500米(自然弯曲忽略不计).(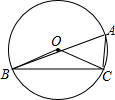 如图,A、B、C三点在⊙O上,∠BAC=60°,若⊙O的半径OC为12,则劣弧BC的长为( )
如图,A、B、C三点在⊙O上,∠BAC=60°,若⊙O的半径OC为12,则劣弧BC的长为( )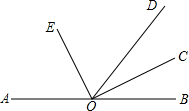 如图,A,O,B三点在同一直线上,OC,OE分别是∠BOD,∠AOD的平分线,OC与OE有什么位置关系?为什么?
如图,A,O,B三点在同一直线上,OC,OE分别是∠BOD,∠AOD的平分线,OC与OE有什么位置关系?为什么?