题目内容
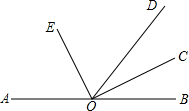 如图,A,O,B三点在同一直线上,OC,OE分别是∠BOD,∠AOD的平分线,OC与OE有什么位置关系?为什么?
如图,A,O,B三点在同一直线上,OC,OE分别是∠BOD,∠AOD的平分线,OC与OE有什么位置关系?为什么?分析:根据角平分线定义得出∠DOE=
∠AOD,∠DOC=
∠DOB,根据∠AOB=∠AOD+∠BOD=180°,求出∠DOE+∠DOC=90°,即可得出答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:OE、OC分别是∠AOD和∠BOD的平分线,
∴∠DOE=
∠AOD,∠DOC=
∠DOB,
∵∠AOB=∠AOD+∠BOD=180°,
∴
(∠AOD+∠BOD)=90°,
即∠DOE+∠DOC=90°,
∴∠EOC=90°,即OC与OE互相垂直.
∴∠DOE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOB=∠AOD+∠BOD=180°,
∴
| 1 |
| 2 |
即∠DOE+∠DOC=90°,
∴∠EOC=90°,即OC与OE互相垂直.
点评:本题考查了角的平分线定义的应用,主要考查学生的计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 9、如图,A、C、E三点在同一条直线上,△DAC和△EBC都是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN.其中,正确结论的个数是( )
9、如图,A、C、E三点在同一条直线上,△DAC和△EBC都是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN.其中,正确结论的个数是( ) 15、如图,A、Q、R三点在一条直线上,S为直线外一点,∠AQS=136°,∠QRS=64°,则∠QSR=( )
15、如图,A、Q、R三点在一条直线上,S为直线外一点,∠AQS=136°,∠QRS=64°,则∠QSR=( )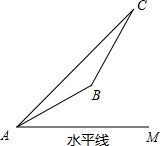 车站B的仰角为30°,AB间缆绳长500米(自然弯曲忽略不计).(
车站B的仰角为30°,AB间缆绳长500米(自然弯曲忽略不计).(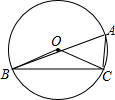 如图,A、B、C三点在⊙O上,∠BAC=60°,若⊙O的半径OC为12,则劣弧BC的长为( )
如图,A、B、C三点在⊙O上,∠BAC=60°,若⊙O的半径OC为12,则劣弧BC的长为( )