题目内容
抛物线y=-x2+(m-1)与y轴交于(0,4)点.
(1)求出抛物线的解析式;
(2)求它与x轴的交点和抛物线顶点的坐标;.
(3)x取什么值时,抛物线在x轴上方?
(4)x取什么值时,y的值随x值的增大而减小?
(1)求出抛物线的解析式;
(2)求它与x轴的交点和抛物线顶点的坐标;.
(3)x取什么值时,抛物线在x轴上方?
(4)x取什么值时,y的值随x值的增大而减小?
考点:抛物线与x轴的交点,二次函数的性质,待定系数法求二次函数解析式
专题:
分析:(1)将点(0,4)代入y=-x2+(m-1),即可得出抛物线的解析式;
(2)令y=0,即可求得它与x轴的交点,再由抛物线的顶点坐标求得答案即可;
(3)根据抛物线和x轴的交点坐标,再由抛物线的开口向下,即可得出x的取值范围;
(4)根据抛物线的性质,抛物线开口向下,在对称轴的左侧,y的值随x值的增大而减小,即可得出x的取值范围.
(2)令y=0,即可求得它与x轴的交点,再由抛物线的顶点坐标求得答案即可;
(3)根据抛物线和x轴的交点坐标,再由抛物线的开口向下,即可得出x的取值范围;
(4)根据抛物线的性质,抛物线开口向下,在对称轴的左侧,y的值随x值的增大而减小,即可得出x的取值范围.
解答:解:(1)把点(0,4)代入y=-x2+(m-1),
得m=5
∴抛物线的解析式为y=-x2+4;
(2)令y=0,得-x2+4=0,解得x=±2,
∴与 x 轴的交点坐标是(-2,0)( 2,0),顶点的坐标( 0,4);
( 3 )∵抛物线的开口向下,
∴当-2<x<2时,抛物线在x轴上方.
( 4 )∵抛物线的开口向下,∴x>0,y的值随 x 值的增大而减小.(或写x≥0也可以)
得m=5
∴抛物线的解析式为y=-x2+4;
(2)令y=0,得-x2+4=0,解得x=±2,
∴与 x 轴的交点坐标是(-2,0)( 2,0),顶点的坐标( 0,4);
( 3 )∵抛物线的开口向下,
∴当-2<x<2时,抛物线在x轴上方.
( 4 )∵抛物线的开口向下,∴x>0,y的值随 x 值的增大而减小.(或写x≥0也可以)
点评:本题考查了抛物线与x轴的交点问题,二次函数的性质以及待定系数法求二次函数的解析式,熟记顶点坐标(-
,
).
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
下列说法正确的是( )
| A、-23a2bc2的系数为-2,次数为8 | ||||||
B、
| ||||||
C、
| ||||||
| D、mx2+1一定是关于x的二次二项式 |
若a=4时,关于x的方程ax+b=0的解是x=2,那么ax-b=0的解是( )
| A、x=2 | ||
| B、x=-2 | ||
C、x=-
| ||
D、x=
|
不等式组
的解集是( )
|
| A、3<x<4 | B、x<4 |
| C、x>3 | D、无解 |

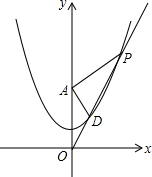 在平面直角坐标系中,有抛物线y=
在平面直角坐标系中,有抛物线y= 如图,四边形ABCD中,AB与CD不平行,点E,F分别是AB、DC的中点,试说明:2EF<AD+BC.
如图,四边形ABCD中,AB与CD不平行,点E,F分别是AB、DC的中点,试说明:2EF<AD+BC.