题目内容
【题目】如图,一次函数y=﹣![]() x+
x+![]() 的图象与反比例函数y=
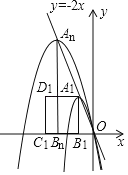
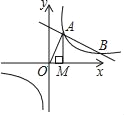
的图象与反比例函数y=![]() (k>0)的图象交于A,B两点,过A点作x轴的垂线,垂足为M,△AOM面积为1.
(k>0)的图象交于A,B两点,过A点作x轴的垂线,垂足为M,△AOM面积为1.
(1)求反比例函数的解析式;
(2)在y轴上求一点P,使PA+PB的值最小,并求出其最小值和P点坐标.
【答案】(1)![]() (2)(0,
(2)(0,![]() )
)
【解析】
(1)根据反比例函数比例系数k的几何意义得出![]() |k|=1,进而得到反比例函数的解析式;
|k|=1,进而得到反比例函数的解析式;
(2)作点A关于y轴的对称点A′,连接A′B,交y轴于点P,得到PA+PB最小时,点P的位置,根据两点间的距离公式求出最小值A′B的长;利用待定系数法求出直线A′B的解析式,得到它与y轴的交点,即点P的坐标.
(1)∵反比例函数 y= =![]() (k>0)的图象过点 A,过 A 点作 x 轴的垂线,垂足为 M,
(k>0)的图象过点 A,过 A 点作 x 轴的垂线,垂足为 M,
∴![]() |k|=1,
|k|=1,
∵k>0,
∴k=2,
故反比例函数的解析式为:y=![]() ;
;
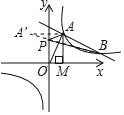
(2)作点 A 关于 y 轴的对称点 A′,连接 A′B,交 y 轴于点 P,则 PA+PB 最小.
由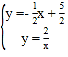 ,解得
,解得![]() ,或
,或![]() ,
,
∴A(1,2),B(4,![]() ),
),
∴A′(﹣1,2),最小值 A′B=![]() =
=![]() ,
,
设直线 A′B 的解析式为 y=mx+n,
则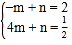 ,解得
,解得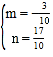 ,
,
∴直线 A′B 的解析式为 y=![]() ,
,
∴x=0 时,y=![]() ,
,
∴P 点坐标为(0,![]() ).
).

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目