题目内容
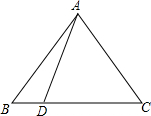如图，D为△ABC中BC边上一点，证明：AD2=AB2•| DC |
| BC |
| BD |
| BC |
| BD |
| BC |
| DC |
| BC |
考点：勾股定理
专题：证明题
分析：过A点做BC垂线 交于E点，则BE=BD+DE，CE=DC-DE，根据勾股定理即可得出AB2•
+AC2•
-BC2•
•
=[AE2+（BD+DE）2]
+[AE2+（DC-DE）2]
-BD•DC，继而即可得出结论．
| DC |
| BC |
| BD |
| BC |
| BD |
| BC |
| DC |
| BC |
| DC |
| BC |
| BD |
| BC |
解答：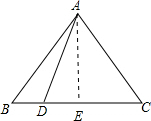
解：过A点做BC垂线 交于E点，则BE=BD+DE，CE=DC-DE，
∵AB2•
+AC2•
-BC2•
•
=[AE2+（BD+DE）2]
+[AE2+（DC-DE）2]
-BD•DC
=AD2•
+
（BD•DC）+
+AD2•
+
（BD•DC）-
-BD•DC
=AD2•（
+
）+（BD•DC）（
+
）-BD•DC
=AD2．
∴AD2=AB2•
+AC2•
-BC2•
•
．
解：过A点做BC垂线 交于E点，则BE=BD+DE，CE=DC-DE，∵AB2•
| DC |
| BC |
| BD |
| BC |
| BD |
| BC |
| DC |
| BC |
=[AE2+（BD+DE）2]
| DC |
| BC |
| BD |
| BC |
=AD2•
| DC |
| BC |
| BD |
| BC |
| 2DE•BD•DC |
| BC |
| BD |
| BC |
| DC |
| BC |
| 2DE•BD•DC |
| BC |
=AD2•（
| BD |
| BC |
| DC |
| BC |
| BD |
| BC |
| DC |
| BC |
=AD2．
∴AD2=AB2•
| DC |
| BC |
| BD |
| BC |
| BD |
| BC |
| DC |
| BC |
点评：本题考查勾股定理的知识，解题关键是利用勾股定理将BE2、CE2化为（BD+DE）2和（DC-DE）2，难度一般．
练习册系列答案
同步练习强化拓展系列答案
相关题目
根据下列表格中列出来的数值，可判断方程x2-bx-c=0有一个根大约是（ ）
| x | 0 | 0.5 | 1 | 1.5 | 2 |
| x2-bx-c | -15 | -8.75 | -2 | 5.25 | 13 |
| A、0.25 | B、0.75 |
| C、1.25 | D、1.75 |
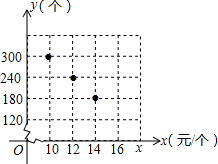某商店准备购进一批茶杯进行销售，根据市场调查，这种茶杯一段时间内的销售量y（个）与销售单价x（元/个）之间的对应关系如图所示：