题目内容
 (2012•白下区一模)如图,山上有一根电线杆,山脚下有一矩形建筑物ABCD,在A、D、C三点测得电线杆顶端F的仰角分别为∠α=48°,∠β=56°,∠γ=65°,测得矩形建筑物宽度AD=20m,高度DC=33m.请你从所测数据中作出选择,计算电线杆顶端到地面的高度FG.(精确到1m)(参考数据:sin48°≈0.7,cos48°≈0.7,tan48°≈1.1,sin56°≈0.8,cos56°≈0.6,tan56°≈1.5,sin65°≈0.9,cos65°≈0.4,tan65°≈2.1)
(2012•白下区一模)如图,山上有一根电线杆,山脚下有一矩形建筑物ABCD,在A、D、C三点测得电线杆顶端F的仰角分别为∠α=48°,∠β=56°,∠γ=65°,测得矩形建筑物宽度AD=20m,高度DC=33m.请你从所测数据中作出选择,计算电线杆顶端到地面的高度FG.(精确到1m)(参考数据:sin48°≈0.7,cos48°≈0.7,tan48°≈1.1,sin56°≈0.8,cos56°≈0.6,tan56°≈1.5,sin65°≈0.9,cos65°≈0.4,tan65°≈2.1)分析:将题目中所涉及到的仰俯角转换为直角三角形内的角,利用解直角三角形的知识求得线段GF的长即可.
解答:解: 解法一:如图,延长AD交FG于点E.…(1分)
解法一:如图,延长AD交FG于点E.…(1分)
在Rt△FDE中,tanβ=
,
∴DE=
.…(2分)
在Rt△FCG中,tanγ=
,
∴CG=
.
…(3分)
∵DE=CG,∴
=
.
∴
=
,
即
=
.
…(5分)
解得FG=
=
=115.5≈116.…(7分)
答:电线杆顶端到地面的高度FG约是116m. …(8分)
解法二:如图,延长AD交FG于点E. …(1分)
在Rt△FDE中,tanβ=
,
∴DE=
. …(2分)
在Rt△FAE中,tanα=
,
∴AE=
.…(3分)
∵AE-DE=AD,
∴
-
=AD. …(5分)
∴FE=
.
∴FG=FE+EG=FE+CD=
+CD=115.5≈116.
…(7分)
答:电线杆顶端到地面的高度FG约是116m. …(8分)
解法三:如图,延长AD交FG于点E. …(1分)
在Rt△FCG中,tanγ=
,
∴CG=
. …(2分)
在Rt△FAE中,tanα=
,
∴AE=
.…(3分)
∵AE-CG=AE-DE=AD,
∴
-
=AD. …(5分)
即
-
=AD.
∴FG=
=115.5≈116.…(7分)
答:电线杆顶端到地面的高度FG约是116m. …(8分)
 解法一:如图,延长AD交FG于点E.…(1分)
解法一:如图,延长AD交FG于点E.…(1分)在Rt△FDE中,tanβ=
| FE |
| DE |
∴DE=
| FE |
| tanβ |
在Rt△FCG中,tanγ=
| FG |
| CG |
∴CG=
| FG |
| tanγ |
…(3分)
∵DE=CG,∴
| FE |
| tanβ |
| FG |
| tanγ |
∴
| FG-EG |
| tanβ |
| FG |
| tanγ |
即
| FG-DC |
| tanβ |
| FG |
| tanγ |
…(5分)
解得FG=
| DC•tanγ |
| tanγ-tanβ |
| 33×2.1 |
| 2.1-1.5 |
答:电线杆顶端到地面的高度FG约是116m. …(8分)
解法二:如图,延长AD交FG于点E. …(1分)
在Rt△FDE中,tanβ=
| FE |
| DE |
∴DE=
| FE |
| tanβ |
在Rt△FAE中,tanα=
| FE |
| AE |
∴AE=
| FE |
| tanα |
∵AE-DE=AD,
∴
| FE |
| tanα |
| FE |
| tanβ |
∴FE=
| AD•tanα•tanβ |
| tanβ-tanα |
∴FG=FE+EG=FE+CD=
| AD•tanα•tanβ |
| tanβ-tanα |
…(7分)
答:电线杆顶端到地面的高度FG约是116m. …(8分)
解法三:如图,延长AD交FG于点E. …(1分)
在Rt△FCG中,tanγ=
| FG |
| CG |
∴CG=
| FG |
| tanγ |
在Rt△FAE中,tanα=
| FE |
| AE |
∴AE=
| FE |
| tanα |
∵AE-CG=AE-DE=AD,
∴
| FE |
| tanα |
| FG |
| tanγ |
即
| FG-CD |
| tanα |
| FG |
| tanγ |
∴FG=
| AD•tanα•tanγ+CD•tanγ |
| tanγ-tanα |
答:电线杆顶端到地面的高度FG约是116m. …(8分)
点评:本题考查了仰俯角问题,解决此类问题的关键是正确的将仰俯角转化为直角三角形的内角并选择正确的边角关系解直角三角形.

练习册系列答案
相关题目
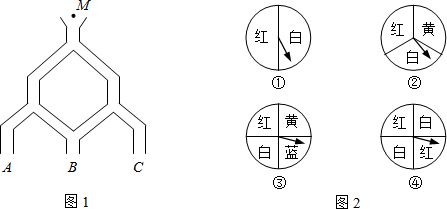
 (2012•白下区一模)如图,三条直线两两相交,交点分别为A、B、C,若∠CAB=50°,∠CBA=60°,则∠1+∠2=
(2012•白下区一模)如图,三条直线两两相交,交点分别为A、B、C,若∠CAB=50°,∠CBA=60°,则∠1+∠2=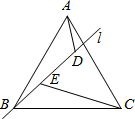 (2012•白下区一模)如图,直线l经过等边三角形ABC的顶点B,在l上取点D、E,使∠ADB=∠CEB=120°.若AD=2cm,CE=5cm,则DE=
(2012•白下区一模)如图,直线l经过等边三角形ABC的顶点B,在l上取点D、E,使∠ADB=∠CEB=120°.若AD=2cm,CE=5cm,则DE=